题目内容
14.函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ<$\frac{π}{2}$)的图象与x轴相邻两个交点间的距离为$\frac{π}{2}$,且图象上一个最低点为M($\frac{2π}{3}$,-2).(Ⅰ)求f(x)的解析式;
(Ⅱ)求f(x)的单调递增区间;
(Ⅲ)当x∈[$\frac{π}{12}$,$\frac{π}{2}$]时,求f(x)的值域.
分析 (Ⅰ)由周期求得ω,由最低点的坐标结合五点法作图求得A及φ的值,可得函数f(x)的解析式.
(Ⅱ)由条件利用正弦函数的单调性,求得f(x)的单调递增区间.
(Ⅲ)当x∈[$\frac{π}{12}$,$\frac{π}{2}$],利用正弦函数的定义域和值域,求得f(x)的值域.
解答 解:(Ⅰ)由图象与x轴相邻两个交点间的距离为$\frac{π}{2}$,$\frac{T}{2}$=$\frac{π}{ω}$=$\frac{π}{2}$,∴ω=2,
再根据图象上一个最低点为M($\frac{2π}{3}$,-2),可得A=2,2×$\frac{2π}{3}$+φ=$\frac{3π}{2}$,φ=$\frac{π}{6}$,
∴f(x)=2sin(2x+$\frac{π}{6}$).
(Ⅱ)令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,求得kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,k∈Z;
(Ⅲ)当x∈[$\frac{π}{12}$,$\frac{π}{2}$]时,$\frac{π}{3}$≤2x+$\frac{π}{6}$≤$\frac{7π}{6}$,∴sin(2x+$\frac{π}{6}$)∈[-1,2],故函数的值域为[-1,2].
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,正弦函数的单调性,正弦函数的定义域和值域,属于基础题.

练习册系列答案
相关题目
2.一个三棱锥的三视图如图所示,则它的体积为( )
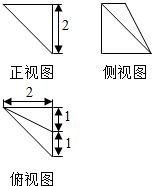

| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | 2 |
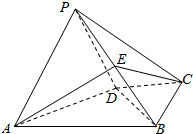 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,∠ABC=90°,AB=2,AD=$\sqrt{2}$,PA=PD=CD=CB=1,E总是线段PB上的动点.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,∠ABC=90°,AB=2,AD=$\sqrt{2}$,PA=PD=CD=CB=1,E总是线段PB上的动点.