题目内容
设数列{an}满足a1=1,a2=4,a3=9,an=an-1+an-2-an-3,n=4,5,…,则a2014= .
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:在数列递推式an=an-1+an-2-an-3中,以n+1替换n,得到an+1=an+an-1-an-2,作和后可得数列{an}的偶数项和偶数项均构成等差数列,由已知求出偶数项的公差,代入等差数列的通项公式求得a2014的值.
解答:
解:由an=an-1+an-2-an-3,得
an+1=an+an-1-an-2,
两式作和得:an+1=2an-1-an-3.
即an+1+an-3=2an-1(n=4,5,…).
∴数列{an}的奇数项和偶数项均构成等差数列,
∵a2=4,a4=12,∴偶数项公差为8.
则a2014=a2+8(1007-1)=4+8×1006=8052.
故答案为:8052.
an+1=an+an-1-an-2,
两式作和得:an+1=2an-1-an-3.
即an+1+an-3=2an-1(n=4,5,…).
∴数列{an}的奇数项和偶数项均构成等差数列,
∵a2=4,a4=12,∴偶数项公差为8.
则a2014=a2+8(1007-1)=4+8×1006=8052.
故答案为:8052.
点评:本题主要考查由递推公式推导数列的通项公式,其中渗透了周期数列这一知识点,属中档题.

练习册系列答案
相关题目
“a≤0”是“函数f(x)=|(ax-1)x|在区间(0,+∞)内单调递增”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
函数f(x)=-x2-4x+1(-3≤x≤3)的值域是( )
| A、(-4,5] |
| B、[-20,4] |
| C、[-20,5] |
| D、[4,5] |
正方体与其外接球的表面积之比为( )
A、
| ||
| B、2:π | ||
| C、3:π | ||
| D、6:π |
设M={x|x2+x+2=0},a=0,则{a}与M的关系是( )
| A、{a}=M |
| B、M?{a} |
| C、{a}?M |
| D、M?{a} |
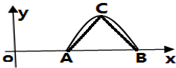 已知函数f(x)=Mcos(ωx+ϕ)(M>0,ω>0,0<ϕ<π)为奇函数,该函数的部分图象如图所示,AC=BC=
已知函数f(x)=Mcos(ωx+ϕ)(M>0,ω>0,0<ϕ<π)为奇函数,该函数的部分图象如图所示,AC=BC=