题目内容
已知锐角在△ABC中,内角A,B,C的对边分别为a,b,c,满足
=
(1)求证:角A,C,B成等差数列;
(2)若△ABC的面积S△ABC=
,求△ABC周长的最小值.
| a+b |
| cosA+cosB |
| c |
| cosC |
(1)求证:角A,C,B成等差数列;
(2)若△ABC的面积S△ABC=
| 3 |
考点:正弦定理,余弦定理
专题:计算题,解三角形
分析:(1)根据题意,由正弦定理得sin(A-C)=sin(C-B)又A、B、C∈(0,
),即有-
<A-C<
,-
<C-B<
,而y=sinx在(-
,
)内单调递增可得A-C=C-B,故可证.
(2)由A+B+C=π及2C=A+B得C=
,由S△ABC=
absinC=
⇒ab=4,由余弦定理得c2=a2+b2-2abcosC=a2+b2-ab,故a+b+c=a+b+
≥2
+
=3
=6,当且仅当a=b时,取等号,从而求解.
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
(2)由A+B+C=π及2C=A+B得C=
| π |
| 3 |
| 1 |
| 2 |
| 3 |
| a2+b2-ab |
| ab |
| 2ab-ab |
| ab |
解答:
解:(1)根据题意,在△ABC中,由正弦定理得:
=
,即有sinAcosC+sinBcosC=sinCcosA+sinCcosB,
∴sin(A-C)=sin(C-B),
又A、B、C∈(0,
),∴-
<A-C<
,-
<C-B<
而y=sinx在(-
,
)内单调递增
∴A-C=C-B
即有2C=A+B,角A,B,C成等差数列.
(2)由A+B+C=π及2C=A+B得C=
,
S△ABC=
absinC=
⇒ab=4,
又c2=a2+b2-2abcosC=a2+b2-ab,
∴a+b+c=a+b+
≥2
+
=3
=6
当且仅当a=b时,取等号
∴△ABC周长的最小值是6.
| sinA+sinB |
| cosA+cosB |
| sinC |
| cosC |
∴sin(A-C)=sin(C-B),
又A、B、C∈(0,
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
而y=sinx在(-
| π |
| 2 |
| π |
| 2 |
∴A-C=C-B
即有2C=A+B,角A,B,C成等差数列.
(2)由A+B+C=π及2C=A+B得C=
| π |
| 3 |
S△ABC=
| 1 |
| 2 |
| 3 |
又c2=a2+b2-2abcosC=a2+b2-ab,
∴a+b+c=a+b+
| a2+b2-ab |
| ab |
| 2ab-ab |
| ab |
当且仅当a=b时,取等号
∴△ABC周长的最小值是6.
点评:本题主要考察了余弦定理和正弦定理的综合应用,不等式的解法,属于中档题.

练习册系列答案
相关题目
如图为一个四棱锥的正视图、侧(左)视图和俯视图,则该四棱锥的表面积为( )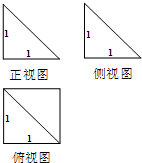

| A、3 | ||
B、2+
| ||
| C、2 | ||
D、3+2
|
“a≤0”是“函数f(x)=|(ax-1)x|在区间(0,+∞)内单调递增”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
函数f(x)=-x2-4x+1(-3≤x≤3)的值域是( )
| A、(-4,5] |
| B、[-20,4] |
| C、[-20,5] |
| D、[4,5] |
已知函数f(x)=sin(ωx+φ)(ω>0,-
<φ<
),其部分图象如图所示,则ω,φ的值分别为( )
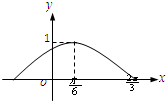
| π |
| 2 |
| π |
| 2 |

A、ω=2,φ=
| ||
B、ω=2,φ=
| ||
C、ω=1,φ=
| ||
D、ω=1,φ=
|
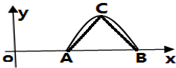 已知函数f(x)=Mcos(ωx+ϕ)(M>0,ω>0,0<ϕ<π)为奇函数,该函数的部分图象如图所示,AC=BC=
已知函数f(x)=Mcos(ωx+ϕ)(M>0,ω>0,0<ϕ<π)为奇函数,该函数的部分图象如图所示,AC=BC=