题目内容
已知数列{an}满足an=
,则数列{an}的前n项和Sn= .
|
考点:数列的求和
专题:等差数列与等比数列
分析:当n为奇数时,Sn=(3+33+35+…+3n)+[2+4+6+…+(n-1)];当n为偶数时,Sn=(3+33+35+…+3n-1)+[2+4+6+…+n].由此能求出数列{an}的前n项和Sn.
解答:
解:当n为奇数时,
Sn=(3+33+35+…+3n)+[2+4+6+…+(n-1)]
=
+
=
+
.
当n为偶数时,
Sn=(3+33+35+…+3n-1)+[2+4+6+…+n]
=
+
=
+
.
∴Sn=
.
故答案为:
.
Sn=(3+33+35+…+3n)+[2+4+6+…+(n-1)]
=
3(1-9
| ||
| 1-9 |
| (n-1)(n+1) |
| 2 |
=
| 3n+2-3 |
| 8 |
| n2-1 |
| 3 |
当n为偶数时,
Sn=(3+33+35+…+3n-1)+[2+4+6+…+n]
=
3(1-9
| ||
| 1-9 |
| ||
| 2 |
=
| 3n+1-3 |
| 8 |
| n(n+2) |
| 4 |
∴Sn=
|
故答案为:
|
点评:本题考查数列的前n项和的求法,是中档题,解题时要注意分类讨论思想的合理运用.

练习册系列答案
相关题目
正方体与其外接球的表面积之比为( )
A、
| ||
| B、2:π | ||
| C、3:π | ||
| D、6:π |
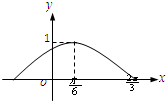
已知函数f(x)=sin(ωx+φ)(ω>0,-
<φ<
),其部分图象如图所示,则ω,φ的值分别为( )
| π |
| 2 |
| π |
| 2 |

A、ω=2,φ=
| ||
B、ω=2,φ=
| ||
C、ω=1,φ=
| ||
D、ω=1,φ=
|
设M={x|x2+x+2=0},a=0,则{a}与M的关系是( )
| A、{a}=M |
| B、M?{a} |
| C、{a}?M |
| D、M?{a} |
下列一次函数中,y随着x增大而减小而的是( )
| A、y=3x |
| B、y=3x-2 |
| C、y=3+2x |
| D、y=-3x-2 |
如果命题“p∨q”为假命题,则( )
| A、p、q均为真命题 |
| B、p、q均为假命题 |
| C、p、q中至少有一个为真命题 |
| D、p、q中至多有一个为真命题 |
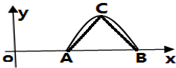 已知函数f(x)=Mcos(ωx+ϕ)(M>0,ω>0,0<ϕ<π)为奇函数,该函数的部分图象如图所示,AC=BC=
已知函数f(x)=Mcos(ωx+ϕ)(M>0,ω>0,0<ϕ<π)为奇函数,该函数的部分图象如图所示,AC=BC=