题目内容
已知正项等比数列{an}满足:a3=4,a4+a5=24.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=
,求数列{bn}的前n项和Sn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=
| an |
| n•(n+1)•2n |
考点:数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)由题意列出方程组求得首项和公比,即可写出通项公式;
(Ⅱ)bn=
=
=
(
-
).利用裂项法求数列的和即可得出结论.
(Ⅱ)bn=
| an |
| n•(n+1)•2n |
| 1 |
| 2n•(n+1) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
解答:
解:(Ⅰ)设正项等比数列{an}的首项为a1,公比为q,
则由a3=4,a4+a5=24得
,
由于an>0,q>0解得
,
所以an=a1•qn-1=2n-1.
(Ⅱ)由an=a1•qn-1=2n-1.得bn=
=
=
(
-
).
∴Sn=
[(
-
)+(
-
)+…+(
-
)]=
(1-
)=
∴Sn=
.
则由a3=4,a4+a5=24得
|
由于an>0,q>0解得
|
所以an=a1•qn-1=2n-1.
(Ⅱ)由an=a1•qn-1=2n-1.得bn=
| an |
| n•(n+1)•2n |
| 1 |
| 2n•(n+1) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
∴Sn=
| 1 |
| 2 |
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| n+1 |
| n |
| 2(n+1) |
∴Sn=
| n |
| 2(n+1) |
点评:本题主要考查等比数列的性质及裂项相消法求数列的和知识,属于中档题、常规题,应熟练掌握.

练习册系列答案
相关题目
方程x2sin2θ+y2cosθ=1表示椭圆,则θ的取值范围( )
A、(2kπ,2kπ+
| ||||||
B、(kπ,kπ+
| ||||||
C、(2kπ,2kπ+
| ||||||
D、(2kπ,2kπ+
|
若(
-
)6展开式中的常数项是60,则实数a的值是( )
| x |
| 2 |
| a | ||
|
| A、±1 | ||
B、±
| ||
| C、±2 | ||
D、±2
|
已知△ABC在中,角A,B,C所对的边分别为a,b,c,且acosC+
c=b,则角A( )
| ||
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
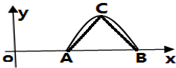 已知函数f(x)=Mcos(ωx+ϕ)(M>0,ω>0,0<ϕ<π)为奇函数,该函数的部分图象如图所示,AC=BC=
已知函数f(x)=Mcos(ωx+ϕ)(M>0,ω>0,0<ϕ<π)为奇函数,该函数的部分图象如图所示,AC=BC=