题目内容

双曲线
x2
a2
-
y2
b2
=1的左右准线l1，l2将线段F1F2三等分，F1，F2分别为双曲线的左右焦点，则双曲线的渐近线方程为（　　）
A、x±
2
y=0
B、y±
2
x=0
C、x±
3
y=0
D、y±
3
x=0
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：首先根据题中的已知条件建立准线间的距离和焦距的关系式，进一步解得
c
a
=
3
，最后求得渐近线方程．
解答： 解：双曲线
x2
a2
-
y2
b2
=1的左右准线l1，l2将线段F1F2三等分，F1，F2分别为双曲线的左右焦点，
则：2×
a2
c
=
2c
3

进一步解得：
c
a
=
3

b
a
=
2

则渐近线方程为y±
2
x=0
故选：B
点评：本题知识考查要点：椭圆的准线方程，焦距的长及椭圆渐进线方程．
练习册系列答案
相关题目
函数f（x）=2|log2x|+1的图象大致是（　　）
A、
B、
C、
D、
若四面体的各棱长是1或2，且该四面体不是正四面体，则其体积不可能是（　　）
A、
11
12
B、
14
12
C、
11
6
D、
3
3
已知函数f（x）=lg（x+
1+x2
）．
（1）求f（x）的定义域；
（2）判断f（x）的奇偶性；
（3）求f（x）的单调区间并证明．
已知函数f1（x）=lg（-x-1）的定义域为M，函数f2（x）=lg（x-3）的定义域为N，A=N∪M，函数g（x）=2x-a（x≤2）的值域为B．
（1）求A、B；
（2）若函数A∩B=B，求实数a的取值范围．
方程x2sin2θ+y2cosθ=1表示椭圆，则θ的取值范围（　　）
A、(2kπ，2kπ+
π
2
)
B、(kπ，kπ+
π
2
)
C、(2kπ，2kπ+
π
6
)
D、(2kπ，2kπ+
π
6
)∪(2kπ+
π
6
，2kπ+
π
2
)k∈Z
设F1，F2分别是椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，若椭圆上存在点A，使∠F1AF2=90°且|AF1|=3|AF2|，则椭圆的离心率为
 
．
已知某个几何体的三视图如图，根据图中标出的尺寸，可得这个几何体的表面积是（　　）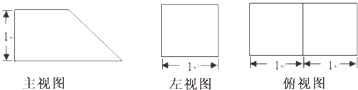
A、
3
2
B、7+
2
C、7+2
2
D、10+
2
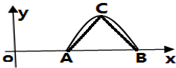已知函数f（x）=Mcos（ωx+ϕ）（M＞0，ω＞0，0＜ϕ＜π）为奇函数，该函数的部分图象如图所示，AC=BC=
2
2
，∠C=90°，则f(
1
2
)=（　　）
A、-
1
2
B、
1
2
C、-
2
2
D、
2
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网