题目内容
函数y=g(x)的图象与函数f(x)=ax-1的图象关于y=x对称,并且g(4)=2,则g(2)的值是( )
A、-
| ||
B、
| ||
| C、2 | ||
| D、4 |
考点:反函数
专题:函数的性质及应用
分析:由函数y=g(x)的图象与函数f(x)=ax-1的图象关于y=x对称,说明g(x)是f(x)的反函数,进一步说明f(x)的图象过(2,4),代入求出a的值后再由函数f(x)的函数值为2求得x的值得答案.
解答:
解:∵函数y=g(x)的图象与函数f(x)=ax-1的图象关于y=x对称,∴g(x)是f(x)的反函数,
由g(4)=2,得f(2)=4,∴a2-1=4,即a=4.
∴f(x)=4x-1,
由4x-1=2,解得:x=
.
∴g(2)=
.
故选:B.
由g(4)=2,得f(2)=4,∴a2-1=4,即a=4.
∴f(x)=4x-1,
由4x-1=2,解得:x=
| 3 |
| 2 |
∴g(2)=
| 3 |
| 2 |
故选:B.
点评:本题考查了函数的反函数,考查了互为反函数的两个函数图象间的关系,是基础题.

练习册系列答案
相关题目
对任意实数a、b、c,给出下列命题:
①“a=b”是“ac=bc”的充要条件;
②“b2=ac”是“a,b,c成等比数列”的充要条件;
③“a<5”是“a<3”的必要条件;
④“a>b”是“a2>b2”的充分条件.
其中真命题的个数是( )
①“a=b”是“ac=bc”的充要条件;
②“b2=ac”是“a,b,c成等比数列”的充要条件;
③“a<5”是“a<3”的必要条件;
④“a>b”是“a2>b2”的充分条件.
其中真命题的个数是( )
| A、4 | B、3 | C、4 | D、1 |
设f(x)=Aisn(ωx+φ),?x1,x2∈R,使f(x1)-f(x2)取得最大值2时,|x1-x2|最小值为π,若f(x)在(
,
)上单调递增,在(
,
)上单调递减,则f(-
)等于( )
| π |
| 4 |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| 8π |
| 3 |
| A、-2 | B、-1 | C、0 | D、1 |
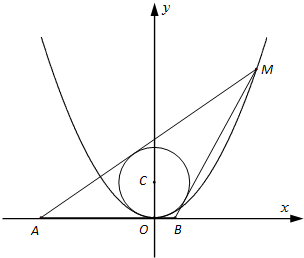 已知圆C:x2+(y-2)2=4,M(x0,y0)为抛物线x2=4y上的动点.
已知圆C:x2+(y-2)2=4,M(x0,y0)为抛物线x2=4y上的动点.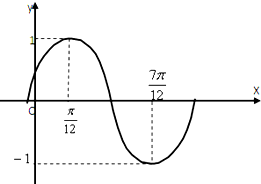 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<