Question

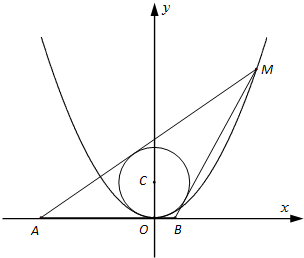已知圆C：x²+（y-2）²=4，M（x₀，y₀）为抛物线x²=4y上的动点．
（1）若x₀=4，求过点M的圆的切线方程；
（2）若x₀＞4，求过点M的圆的两切线与x轴围成的三角形面积S的最小值．

Answer 1

考点：直线与圆锥曲线的关系,圆的切线方程

专题：圆锥曲线的定义、性质与方程

分析：（Ⅰ）设切线方程为y-4=k（x-4），利用圆心到切线的距离等于半径，求出k．然后求出切线方程．
（Ⅱ）设切线y-y₀=k（x-x₀），利用切线与x轴交点为(x0-

y0

k

，0)，圆心到切线的距离列出关系式，推出k的二次方程，设两切线斜率分别为k₁，k₂，通过韦达定理得到

k1+k2=- 2x0(2-y0) x 2 0 -4 k1k2= y 2 0 -4y0 x 2 0 -4

，表示出三角形的面积，利用基本不等式求出最小值．

解答： 解：（Ⅰ）x₀=4，y₀=4．
当点M（4，4）时，设切线方程为y-4=k（x-4），即kx-y+4-4k=0．
圆心到切线的距离为d=

|2-4k|

k2+1

=2，即|2-4k|=2

k2+1

．
所以3k²-4k=0，得k=0或k=

4

3

．
所以切线方程为y=4或4x-3y-4=0．…（6分）
（Ⅱ）设切线y-y₀=k（x-x₀），即kx-y+y₀-kx₀=0，
切线与x轴交点为(x0-

y0

k

，0)，圆心到切线的距离为d=

|-2+y0-kx0|

k2+1

=2．
即4+

y

2 0

+k2

x

2 0

-4y0+4kx0-2x0y0k=0，
化简得(

x

2 0

-4)k2+2x0(2-y0)k+

y

2 0

-4y0=0
设两切线斜率分别为k₁，k₂，则

k1+k2=- 2x0(2-y0) x 2 0 -4 k1k2= y 2 0 -4y0 x 2 0 -4

，S=

1

2

|(x0-

y0

k1

)-(x0-

y0

k2

)|•y0=

1

2

|k1-k2|

|k1k2|

•y02=

2y0 x 2 0 + y 2 0 -4y0

y0-4

=

2y02

y0-4

=2[

16

y0-4

+(y0-4)+8]≥32，当且仅当y₀=8时取等号．
所以两切线与x轴围成的三角形面积S的最小值为32．…（15分）

点评：本题考查圆的方程的求法，直线与圆的位置关系，以及直线与圆锥曲线的位置关系的应用，考查计算能力．