题目内容
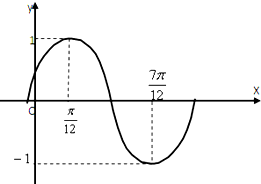已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜| π |
| 2 |
（1）求函数f（x）的解析式，并写出f（x）的单调减区间；
（2）记△ABC的内角A，B，C的对边长分别为a，b，c，若f（A）=1，cosB=
| 4 |
| 5 |
考点：由y=Asin（ωx+φ）的部分图象确定其解析式,函数y=Asin（ωx+φ）的图象变换,正弦定理
专题：三角函数的图像与性质,解三角形
分析：（1）由函数图象向左平移
得到函数f（x）=Asin（ωx+ϕ），（A＞0，ω＞0，|ϕ|＜
）的部分图象，由图象最高点得A=1，由周期可求ω的值，根据特殊点可求ϕ的值，从而可得解析式f（x）=sin（2x+
），从而可求f（x）的单调减区间．
（2）先求范围
＜2A+
＜
，由2A+
=
，可求sinB的值，由正弦定理可求b的值．
| π |
| 12 |
| π |
| 2 |
| π |
| 3 |
（2）先求范围
| π |
| 3 |
| π |
| 3 |
| 7π |
| 3 |
| π |
| 3 |
| π |
| 2 |
解答：
解：（1）由函数图象向左平移
得到函数f（x）=Asin（ωx+ϕ），（A＞0，ω＞0，|ϕ|＜
）的部分图象，由图象最高点得A=1，
由周期
T=（
+
）-（
+
）=
，T=π，∴ω=2．（2分）
当x=
时，f（x）=1，可得 sin（2•
+ϕ）=1，
∵|ϕ|＜
，∴ϕ=
．∴f（x）=sin（2x+
）．（4分）
由图象可得f（x）的单调减区间为[kπ+
，kπ+
]，k∈Z．（6分）
（2）由（I）可知，sin（2A+
）=1，
∵0＜A＜π，∴
＜2A+
＜
，∴2A+
=
，A=
．
∵0＜B＜π，∴sinB=
=
．（9分）
由正弦定理得
=
⇒b=3（
+
）．（12分）
| π |
| 12 |
| π |
| 2 |
由周期
| 1 |
| 2 |
| 7π |
| 12 |
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
| π |
| 2 |
当x=
| π |
| 12 |
| π |
| 12 |
∵|ϕ|＜
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
由图象可得f（x）的单调减区间为[kπ+
| π |
| 12 |
| 7π |
| 12 |
（2）由（I）可知，sin（2A+
| π |
| 3 |
∵0＜A＜π，∴
| π |
| 3 |
| π |
| 3 |
| 7π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
∵0＜B＜π，∴sinB=
| 1+cos2B |
| 3 |
| 5 |
由正弦定理得
| a |
| sinA |
| b |
| sinB |
| 6 |
| 2 |
点评：本题主要考查了由y=Asin（ωx+φ）的部分图象确定其解析式，函数y=Asin（ωx+φ）的图象变换，正弦定理的应用，属于基本知识的考查．
练习册系列答案
相关题目
“m=2“是“f（x）=x2+2（m2-m-2）x+2”为偶函数”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设z=
+(1+i)2，则|z|=（ ）
| 2 |
| 1+i |
A、
| ||
| B、1 | ||
| C、2 | ||
D、
|
函数y=g（x）的图象与函数f（x）=ax-1的图象关于y=x对称，并且g（4）=2，则g（2）的值是（ ）
A、-
| ||
B、
| ||
| C、2 | ||
| D、4 |