题目内容
20.($\frac{2}{x}$+x+1)(1-2$\sqrt{x}$+x)4的展开式中x的系数是169(用数字作答).分析 ($\frac{2}{x}$+x+1)(1-2$\sqrt{x}$+x)4=($\frac{2}{x}$+x+1)$(\sqrt{x}-1)^{8}$.$(\sqrt{x}-1)^{8}$的展开式的通项公式:Tr+1=${∁}_{8}^{r}$(-1)8-r$(\sqrt{x})^{r}$=${∁}_{8}^{r}$(-1)8-r${x}^{\frac{r}{2}}$.令$\frac{r}{2}$=2,0,1,分别解得r,进而得出.
解答 解:($\frac{2}{x}$+x+1)(1-2$\sqrt{x}$+x)4=($\frac{2}{x}$+x+1)$(\sqrt{x}-1)^{8}$.
$(\sqrt{x}-1)^{8}$的展开式的通项公式:Tr+1=${∁}_{8}^{r}$(-1)8-r$(\sqrt{x})^{r}$=${∁}_{8}^{r}$(-1)8-r${x}^{\frac{r}{2}}$.
令$\frac{r}{2}$=2,0,1,分别解得r=4,0,2.
∴($\frac{2}{x}$+x+1)(1-2$\sqrt{x}$+x)4的展开式中x的系数=2×${∁}_{8}^{4}×(-1)^{4}$+${∁}_{8}^{0}$(-1)8+${∁}_{8}^{2}(-1)^{6}$=169.
故答案为:169.
点评 本题考查了二项式定理的通项公式及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.设函数f(x)=$\left\{\begin{array}{l}{lo{g}_{0.2}x,x∈(1,+∞)}\\{2-2x,x∈(-∞,1]}\end{array}\right.$,若a=f(20.3),b=f(log0.32),c=f(log32),则a、b、c的大小关系是( )
| A. | b>c>a | B. | b>a>c | C. | a>c>b | D. | a>b>c |
7.已知2a+2b=2c,则a+b-2c的最大值等于( )
| A. | -2 | B. | -1 | C. | $\frac{1}{4}$ | D. | -$\frac{1}{4}$ |
8.已知3cos2θ=tanθ+3,且θ≠kπ(k∈Z),则sin[2(π-θ)]等于( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
5.已知复数m=4-xi,n=3+2i,若复数$\frac{n}{m}$∈R,则实数x的值为( )
| A. | -6 | B. | 6 | C. | $\frac{8}{3}$ | D. | -$\frac{8}{3}$ |
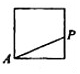
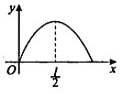 动点P从点A出发,按逆时针方向沿周长为1的平面图形运动一周,A,P两点间的距离y与动点P所走过的路程x的关系如图所示,那么动点P所走的图形可能是( )
动点P从点A出发,按逆时针方向沿周长为1的平面图形运动一周,A,P两点间的距离y与动点P所走过的路程x的关系如图所示,那么动点P所走的图形可能是( )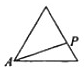
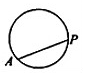
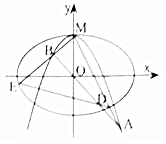 如图,抛物线C1:y=b-x2经过椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点及上顶点M,过点M的两条互相垂直的直线l1,l2分别交抛物线于A,B两点,交椭圆于D,E两点,已知抛物线C1:y=b-x2与x轴所围成的区域面积为$\frac{4}{3}$.
如图,抛物线C1:y=b-x2经过椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点及上顶点M,过点M的两条互相垂直的直线l1,l2分别交抛物线于A,B两点,交椭圆于D,E两点,已知抛物线C1:y=b-x2与x轴所围成的区域面积为$\frac{4}{3}$.