题目内容

18．已知a＞0，b＞0，用分析法证明：$\frac{a+b}{2}$≥$\frac{2ab}{a+b}$．

分析 利用分析法（执果索因），要证$\frac{a+b}{2}$≥$\frac{2ab}{a+b}$，只需证明（a-b）2≥0即可，该式显然成立．

解答 证明：因为a＞0，b＞0，要证$\frac{a+b}{2}$≥$\frac{2ab}{a+b}$，
只要证，（a+b）2≥4ab，只要证（a+b）2-4ab≥0，
即证a2-2ab+b2≥0，
而a2-2ab+b2=（a-b）2≥0恒成立，
故$\frac{a+b}{2}$≥$\frac{2ab}{a+b}$成立．

点评 本题考查不等式的证明，着重考查分析法的应用，考查推理能力，属于中档题．

练习册系列答案
相关题目
8．对甲、乙两名自行车赛手在相同条件下进行了6次测试，测得他们的最大速度（单位：m/s）的数据如下：
甲273830373531
乙332938342836
（1）画出茎叶图，由茎叶图你能获得哪些信息？
（2）分别求出甲、乙两名自行车赛手最大速度（m/s）数据的平均数、极差、方差，并判断选谁参加比赛比较合适？
9．下列命题正确的是（　　）
A．若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|，则$\overrightarrow{a}$=$\overrightarrow{b}$B．若|$\overrightarrow{a}$|＞|$\overrightarrow{b}$|，则$\overrightarrow{a}$＞$\overrightarrow{b}$C．若$\overrightarrow{a}$=$\overrightarrow{b}$，则$\overrightarrow{a}$∥$\overrightarrow{b}$D．若|$\overrightarrow{a}$|=0，则$\overrightarrow{a}$=0
6．球的半径扩大为原来的2倍，它的体积扩大为原来的（　　）倍．
A．4B．8C．16D．64
13．在等差数列{an}中，
（1）已知a6=10，S5=5，求Sn；
（2）已知前3项和为12，前3项积为48，且d＞0，求a1．
3．我国古代数学名著《数书九章》有“米谷粒分”题：粮仓开仓收粮，有人送来米1533石，验得米内夹谷，抽样取米一把，数得254粒内夹谷56粒，则这批米内夹谷约为（　　）
A．1365石B．338石C．168石D．134石
10．若某个扇形的半径为3cm，弧长为πcm，则该扇形的面积为（　　）
A．πcm2B．$\frac{3}{2}π$cm2C．3πcm2D．6πcm2
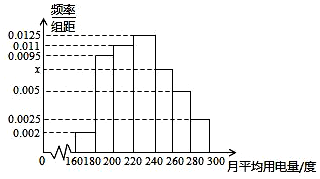7．某城市100户居民的月平均用电量（单位：度），以[160，180），[180，200），[200，220），[220，240），[240，260），[260，280），[280，300]分组的频率分布直方图如图示．
（1）求直方图中x的值；
（2）求月平均用电量的众数和中位数；
（3）在月平均用电量为[220，240），[240，260），[260，280），[280，300]的四组用户中，用分层抽样的方法抽取11户居民，则月平均用电量在[220，240）的用户中应抽取多少户？
8．已知集合A={-2，-1，0，1，2}，∁RB={x|$\frac{x-1}{x+2}$≥0}，则A∩B=（　　）
A．{-1，0，1}B．{-1，0}C．{-2，-1，0}D．{0，1，2}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网