题目内容
8.已知集合A={-2,-1,0,1,2},∁RB={x|$\frac{x-1}{x+2}$≥0},则A∩B=( )| A. | {-1,0,1} | B. | {-1,0} | C. | {-2,-1,0} | D. | {0,1,2} |
分析 解不等式求出∁RB,根据补集与交集的定义计算即可.
解答 解:集合A={-2,-1,0,1,2},
∁RB={x|$\frac{x-1}{x+2}$≥0}={x|x<-2或x≥1},
∴B={x|-2≤x<1}
则A∩B={-2,-1,0}.
故选:C.
点评 本题考查了集合的运算与解不等式的应用问题,是基础题.

练习册系列答案
相关题目
16.已知椭圆的方程为$\frac{x^2}{6}+\frac{y^2}{2}=1$,A是其右顶点,B是该椭圆在第一象限部分上的一点,且$∠AOB=\frac{π}{4}$,若点C是椭圆上的动点,则$\overrightarrow{OA}•\overrightarrow{BC}$的取值范围为( )
| A. | [-3,3] | B. | [-9,3] | C. | $[-2-\sqrt{3}\;,\;2-\sqrt{3}]$ | D. | $[-3\sqrt{3}\;,\;3]$ |
13.已知圆C:x2+y2=1,点P为直线$\frac{x}{4}$+$\frac{y}{2}$=1上一动点,过点P向圆C引两条切线PA,PB,A,B为切点,则直线AB经过定点( )
| A. | $({\frac{1}{2},\frac{1}{4}})$ | B. | $({\frac{1}{4},\frac{1}{2}})$ | C. | $({\frac{{\sqrt{3}}}{4},0})$ | D. | $({0,\frac{{\sqrt{3}}}{4}})$ |
 如图一个水平放置的无盖透明的正方体容器,高12cm,将一个球放在容器口,在向容器内注水,当球面恰好接触水面时测得水深为8cm,如果不计容器厚度,则球的体积为$\frac{2197π}{6}$cm3.
如图一个水平放置的无盖透明的正方体容器,高12cm,将一个球放在容器口,在向容器内注水,当球面恰好接触水面时测得水深为8cm,如果不计容器厚度,则球的体积为$\frac{2197π}{6}$cm3.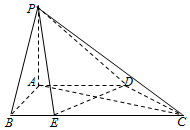 如图,在四棱锥P-ABCD中,AD∥BC,AB⊥AD,PA⊥平面ABCD,点E在BC上,BC=2AB=2AD=4BE.
如图,在四棱锥P-ABCD中,AD∥BC,AB⊥AD,PA⊥平面ABCD,点E在BC上,BC=2AB=2AD=4BE.