题目内容
3.我国古代数学名著《数书九章》有“米谷粒分”题:粮仓开仓收粮,有人送来米1533石,验得米内夹谷,抽样取米一把,数得254粒内夹谷56粒,则这批米内夹谷约为( )| A. | 1365石 | B. | 338石 | C. | 168石 | D. | 134石 |
分析 设这批米内夹谷约为x石,由题意列出方程,由此能求出这批米内夹谷的数量.
解答 解:设这批米内夹谷约为x石,
由题意得$\frac{x}{1533}=\frac{56}{254}$,
解得x≈338.
∴这批米内夹谷约为338石.
故选:B.
点评 本题考查概率的应用,是基础题,解题时要认真审题,注意概率意义的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.直三棱柱ABC-A1B1C1中,∠BAC=90°,M,N分别是A1B1,A1C1的中点,BA=CA=CC1,则BM与AN所成角的余弦值为( )
| A. | $\frac{4}{5}$ | B. | $\frac{1}{10}$ | C. | $\frac{{3\sqrt{10}}}{10}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
14.已知函数f(x)=ax3-3x2+3x,若f'(x)存在唯一的零点x0,且x0>0,则a的值是( )
| A. | 2或1 | B. | 0 | C. | 1或0 | D. | 1 |
8.在等差数列{an}中,a1=10,公差为d,前 n项和为Sn,当且仅当n=5 时Sn取得最大值,则d 的取值范围为( )
| A. | $(-\frac{5}{2},-2)$ | B. | $(-∞,-\frac{5}{2}]$ | C. | (-∞,-2] | D. | $[-\frac{5}{2},-2]$ |
13.已知圆C:x2+y2=1,点P为直线$\frac{x}{4}$+$\frac{y}{2}$=1上一动点,过点P向圆C引两条切线PA,PB,A,B为切点,则直线AB经过定点( )
| A. | $({\frac{1}{2},\frac{1}{4}})$ | B. | $({\frac{1}{4},\frac{1}{2}})$ | C. | $({\frac{{\sqrt{3}}}{4},0})$ | D. | $({0,\frac{{\sqrt{3}}}{4}})$ |

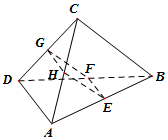 (文科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,
(文科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,