题目内容
4.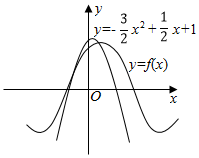 如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}}$)离y轴最近的零点与最大值均在抛物线y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1上,则f(x)=( )
如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}}$)离y轴最近的零点与最大值均在抛物线y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1上,则f(x)=( )| A. | $f(x)=sin(\frac{1}{6}x+\frac{π}{3})$ | B. | $f(x)=sin(\frac{1}{2}x+\frac{π}{3})$ | C. | $f(x)=sin(\frac{π}{2}x+\frac{π}{3})$ | D. | $f(x)=sin(\frac{π}{2}x+\frac{π}{6})$ |
分析 根据题意,令y=0,求出点(-$\frac{2}{3}$,0)在函数f(x)的图象上,再令y=1,求出点($\frac{1}{3}$,1)在函数f(x)的图象上,从而求出φ与ω的值,即可得出f(x)的解析式.
解答 解:【解法一】根据题意,令y=0,得-$\frac{3}{2}$x2+$\frac{1}{2}$x+1=0,
解得x=-$\frac{2}{3}$或x=1;
∴点(-$\frac{2}{3}$,0)在函数f(x)的图象上,
令y=1,解得x=0或x=$\frac{1}{3}$,
∴点($\frac{1}{3}$,1)在函数f(x)的图象上,
∴T=4;
∴ω=$\frac{2π}{T}$=$\frac{π}{2}$;
由($\frac{1}{3}$,1)在f(x)的图象上,得sin($\frac{π}{2}$×$\frac{1}{3}$+φ)=1,
∴$\frac{π}{6}$+φ=2kπ+$\frac{π}{2}$,k∈Z;
又|φ|<$\frac{π}{2}$,
∴k=0时,φ=$\frac{π}{3}$.
∴f(x)=sin($\frac{π}{2}$x+$\frac{π}{3}$).
故选:C.
【解法二】函数f(x)离y轴最近的零点与最大值均在抛物线$y=-\frac{3}{2}{x^2}+\frac{1}{2}x+1$上,
令y=0,得-$\frac{3}{2}$x2+$\frac{1}{2}$x+1=0,
解得x=-$\frac{2}{3}$或x=1;
∴点(-$\frac{2}{3}$,0)在函数f(x)的图象上,
∴-$\frac{2}{3}$ω+φ=0,即φ=$\frac{2}{3}$ω①;
又令ωx+φ=$\frac{π}{2}$,得ωx=$\frac{π}{2}$-φ②;
把①代入②得,x=$\frac{π}{2ω}$-$\frac{2}{3}$③;
令y=1,得-$\frac{3}{2}$x2+$\frac{1}{2}$x+1=1,
解得x=0或x=$\frac{1}{3}$;
即$\frac{π}{2ω}$-$\frac{2}{3}$=$\frac{1}{3}$,
解得ω=$\frac{1}{2}$π,
∴φ=$\frac{2}{3}$ω=$\frac{π}{3}$,
∴f(x)=sin($\frac{π}{2}$x+$\frac{π}{3}$).
故选:C.
点评 本题考查了解函数y=sin(ωx+φ)以及二次函数的图象与性质的应用问题,是基础题目.

| A. | 0 | B. | 2 | C. | -2 | D. | $\frac{1}{2}$ |
| A. | {x|0<x<3} | B. | {x|-1<x<0} | C. | {x|-2<x<0} | D. | {x|-3<x<3} |
| A. | $-\frac{{\sqrt{6}}}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $-\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
 如图所示,在△ABC所在平面外有一点P,M、N分别是PC和AC上的点,过MN作平面平行于BC,画出这个平面与其他各面的交线,并说明画法.
如图所示,在△ABC所在平面外有一点P,M、N分别是PC和AC上的点,过MN作平面平行于BC,画出这个平面与其他各面的交线,并说明画法.