题目内容
19．设集合A={x|x2-x-6＜0，x∈R}，B={y|y=|x|-3，x∈A}，则A∩B等于（ ）| A． | {x|0＜x＜3} | B． | {x|-1＜x＜0} | C． | {x|-2＜x＜0} | D． | {x|-3＜x＜3} |
分析 分别求出关于集合A、B的范围，取交集即可．
解答 解：∵A={x|x2-x-6＜0，x∈R}={x|-2＜x＜3}=（-2，3），
B={y|y=|x|-3，x∈A}=[-3，0），
则A∩B=（-2，0），
故选：C．
点评 本题考查了交集的运算．考查解不等式问题，是一道基础题．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
4．
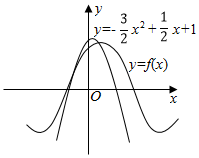如图所示，函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}}$）离y轴最近的零点与最大值均在抛物线y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1上，则f（x）=（ ）
如图所示，函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}}$）离y轴最近的零点与最大值均在抛物线y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1上，则f（x）=（ ）| A． | $f（x）=sin（\frac{1}{6}x+\frac{π}{3}）$ | B． | $f（x）=sin（\frac{1}{2}x+\frac{π}{3}）$ | C． | $f（x）=sin（\frac{π}{2}x+\frac{π}{3}）$ | D． | $f（x）=sin（\frac{π}{2}x+\frac{π}{6}）$ |
9．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为$\frac{\sqrt{5}}{2}$，过右焦点的直线与两条渐近线分别交于A，B，且与其中一条渐近线垂直，若△OAB的面积为$\frac{16}{3}$，其中O为坐标原点，则双曲线的焦距为（ ）
| A． | 2$\sqrt{3}$ | B． | 2$\sqrt{5}$ | C． | 2$\sqrt{10}$ | D． | 2$\sqrt{15}$ |