题目内容
16.已知△ABC中,边a,b,c的对角分别为A,B,C,且$a=\sqrt{6}$,$c=\sqrt{2}$,$A=\frac{2π}{3}$.(Ⅰ)求B,C及△ABC的面积;
(Ⅱ)已知函数f(x)=sinBsin2πx+cosCcos2πx,把函数y=f(x)的图象向右平移$\frac{1}{4}$个单位,然后把所得函数图象上点的横坐标伸长为原来的2倍,纵坐标不变,即得函数y=g(x)的图象,求函数y=g(x)在[0,2]上的单调递增区间.
分析 (Ⅰ)由已知及正弦定理可求sinC=$\frac{1}{2}$,结合C,B为锐角,可得C,B,b的值,利用三角形面积公式即可计算得解.
(Ⅱ)利用三角函数恒等变换的应用化简可得函数解析式f(x)=sin(2πx+$\frac{π}{3}$),利用函数y=Asin(ωx+φ)的图象变换可得g(x)=sin(πx-$\frac{π}{6}$),利用正弦函数的单调性求得函数的增区间,再结合x∈[0,2],可得结论.
解答 解:(Ⅰ)∵$a=\sqrt{6}$,$c=\sqrt{2}$,$A=\frac{2π}{3}$,
∴由正弦定理$\frac{c}{sinC}=\frac{a}{sinA}$,可得:sinC=$\frac{csinA}{a}$=$\frac{\sqrt{2}×\frac{\sqrt{3}}{2}}{\sqrt{6}}$=$\frac{1}{2}$,
∵C,B为锐角,可得:C=$\frac{π}{6}$,B=π-A-C=$\frac{π}{6}$,b=c=$\sqrt{2}$
∴S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}×\sqrt{2}×\sqrt{2}×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$.
(Ⅱ)∵B=$C=\frac{π}{6}$,
∴f(x)=sinBsin2πx+cosCcos2πx=$\frac{1}{2}$sin2πx+$\frac{\sqrt{3}}{2}$cos2πx=sin(2πx+$\frac{π}{3}$),
∴把函数y=f(x)的图象向右平移$\frac{1}{4}$个单位,可得函数解析式:y=sin[2π(x-$\frac{1}{4}$)+$\frac{π}{3}$]=sin(2πx-$\frac{π}{6}$),
然后把所得函数图象上点的横坐标伸长为原来的2倍,纵坐标不变,即得函数y=g(x)=sin(πx-$\frac{π}{6}$),
∴由2kπ-$\frac{π}{2}$≤πx-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z,解得2k$-\frac{1}{3}$≤x≤2k+$\frac{2}{3}$,k∈Z
∵x∈[0,2],
∴可得函数的增区间为[0,$\frac{2}{3}$]∪[$\frac{5}{3}$,2].
点评 本题主要考查了正弦定理,三角形面积公式,三角函数恒等变换的应用,函数y=Asin(ωx+φ)的图象变换,正弦函数的图象和性质的应用,考查了转化思想和数形结合思想,属于中档题.

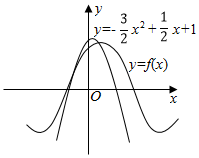 如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}}$)离y轴最近的零点与最大值均在抛物线y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1上,则f(x)=( )
如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}}$)离y轴最近的零点与最大值均在抛物线y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1上,则f(x)=( )| A. | $f(x)=sin(\frac{1}{6}x+\frac{π}{3})$ | B. | $f(x)=sin(\frac{1}{2}x+\frac{π}{3})$ | C. | $f(x)=sin(\frac{π}{2}x+\frac{π}{3})$ | D. | $f(x)=sin(\frac{π}{2}x+\frac{π}{6})$ |
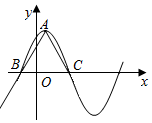 函数f(x)=6cos2$\frac{ωx}{2}$+$\sqrt{3}$sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.
函数f(x)=6cos2$\frac{ωx}{2}$+$\sqrt{3}$sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.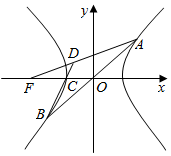 如图,双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)左焦点、左顶点分别为F,C,过原点O的直线与两分支分别交于A,B(异于C点),若直线AF交BC于D点,且$\overrightarrow{AD}$=2$\overrightarrow{DF}$,则双曲线的离心率为( )
如图,双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)左焦点、左顶点分别为F,C,过原点O的直线与两分支分别交于A,B(异于C点),若直线AF交BC于D点,且$\overrightarrow{AD}$=2$\overrightarrow{DF}$,则双曲线的离心率为( )