题目内容
13.已知数列{an}是等差数列,an+1>an,a1•a10=160,a3+a8=37.(1)求数列{an}的通项公式;
(2)若从数列{an}中依次取出第2项,第4项,第8项,第2n项,按原来的顺序组成一个新数列{bn},求Sn=b1+b2+…+bn.
分析 (1)设等差数列{an}的公差为d,由an+1>an,a1•a10=160,a3+a8=37.利用等差数列的通项公式即可得出.
(2)bn=${a}_{{2}^{n}}$=3×2n+2.再利用等比数列的前n项和公式即可得出.
解答 解:(1)设等差数列{an}的公差为d,∵an+1>an,a1•a10=160,a3+a8=37.
∴$\left\{\begin{array}{l}{{a}_{1}({a}_{1}+9d)=160}\\{2{a}_{1}+9d=37}\end{array}\right.$,化为${a}_{1}^{2}$-37a1+160=0,
解得a1=32,或5.
∴$\left\{\begin{array}{l}{{a}_{1}=32}\\{d=-3}\end{array}\right.$(舍去),$\left\{\begin{array}{l}{{a}_{1}=5}\\{d=3}\end{array}\right.$.
∴an=5+3(n-1)=3n+2.
(2)bn=${a}_{{2}^{n}}$=3×2n+2.
∴Sn=b1+b2+…+bn=3(21+22+…+2n)+2n
=$3×\frac{2({2}^{n}-1)}{2-1}$+2n
=3×2n+1-6+2n.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
4.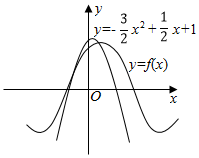 如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}}$)离y轴最近的零点与最大值均在抛物线y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1上,则f(x)=( )
如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}}$)离y轴最近的零点与最大值均在抛物线y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1上,则f(x)=( )
 如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}}$)离y轴最近的零点与最大值均在抛物线y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1上,则f(x)=( )
如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}}$)离y轴最近的零点与最大值均在抛物线y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1上,则f(x)=( )| A. | $f(x)=sin(\frac{1}{6}x+\frac{π}{3})$ | B. | $f(x)=sin(\frac{1}{2}x+\frac{π}{3})$ | C. | $f(x)=sin(\frac{π}{2}x+\frac{π}{3})$ | D. | $f(x)=sin(\frac{π}{2}x+\frac{π}{6})$ |
5.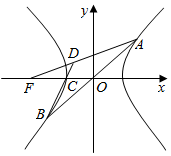 如图,双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)左焦点、左顶点分别为F,C,过原点O的直线与两分支分别交于A,B(异于C点),若直线AF交BC于D点,且$\overrightarrow{AD}$=2$\overrightarrow{DF}$,则双曲线的离心率为( )
如图,双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)左焦点、左顶点分别为F,C,过原点O的直线与两分支分别交于A,B(异于C点),若直线AF交BC于D点,且$\overrightarrow{AD}$=2$\overrightarrow{DF}$,则双曲线的离心率为( )
 如图,双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)左焦点、左顶点分别为F,C,过原点O的直线与两分支分别交于A,B(异于C点),若直线AF交BC于D点,且$\overrightarrow{AD}$=2$\overrightarrow{DF}$,则双曲线的离心率为( )
如图,双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)左焦点、左顶点分别为F,C,过原点O的直线与两分支分别交于A,B(异于C点),若直线AF交BC于D点,且$\overrightarrow{AD}$=2$\overrightarrow{DF}$,则双曲线的离心率为( )| A. | 2 | B. | 3 | C. | 4 | D. | $\frac{3}{2}$ |
3.已知F为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,且双曲线C的焦距为2c,定点G(0,c),若双曲线C上存在点P满足|PF|=|PG|,则双曲线的离心率的取值范围是( )
| A. | ($\sqrt{2}$,+∞) | B. | (1,$\sqrt{2}$) | C. | [$\sqrt{3}$,+∞) | D. | (1,$\sqrt{3}$) |
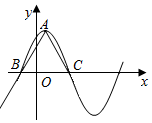 函数f(x)=6cos2$\frac{ωx}{2}$+$\sqrt{3}$sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.
函数f(x)=6cos2$\frac{ωx}{2}$+$\sqrt{3}$sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.