题目内容
19.已知函数f(x)=lnx+$\frac{a}{x}$.(1)当a<0时,证明函数f(x)在(0,+∞)是单调函数;
(2)当a<e时,函数f(x)在区间[1,e]上的最小值是$\frac{4}{3}$,求a的值;
(3)设g(x)=f(x)-$\frac{a}{x}$,A,B是函数g(x)图象上任意不同的两点,记线段AB的中点的横坐标是x0,证明直线AB的斜率k>g'(x0).
分析 (1)求出f'(x),讨论其符号,确定单调区间
(2)在[1,e]上,分如下情况讨论:当1<a<e时,a≤1时,求出最值,列式计算,
(3)$g'({x_0})=\frac{2}{{{x_1}+{x_2}}}$.又$k=\frac{{g({x_2})-g({x_1})}}{{{x_2}-{x_1}}}=\frac{{ln\frac{x_2}{x_1}}}{{{x_2}-{x_1}}}$,不妨设x2>x1,要比较k与g'(x0)的大小,即比较$\frac{ln\frac{{x}_{2}}{{x}_{1}}}{\frac{{x}_{1}}{{x}_{2}-{x}_{1}}}$与$\frac{2}{{x}_{1}+{x}_{2}}$的大小,又因为x2>x1,令h(x)=lnx-$\frac{2(x-1)}{x+1},(x>1)$,则h′(x)=$\frac{(x-1)^{2}}{x(x+1)^{2}}≥0$根据h(x)在[1,+∞)上的单调性即可得出结论.
解答 (1)解:$f'(x)=\frac{x-a}{x^2}$.
因为a<0,x>0,所以f'(x)>0.∴函数f(x)在(0,+∞)是单增函数;…(2分)
(2)解:在[1,e]上,分如下情况讨论:当1<a<e时,函数f(x)在[1,a)上有f'(x)<0,单调递减,在(a,e]上有f'(x)>0,单调递增,
∴函数f(x)的最小值为$f(a)=lna+1=\frac{4}{3}$,得$a={e^{\frac{1}{3}}}$.…(8分)
当a≤1时,函数f(x)在[1,e]上有f'(x)>0,单调递增,∴函数f(x)的最小值为f(1)=a=$\frac{3}{3}$>1,故不存在
综上,得$a={e^{\frac{1}{3}}}$.
(3)证明:$g(x)=lnx,g'(x)=\frac{1}{x}$,$g'({x_0})=\frac{2}{{{x_1}+{x_2}}}$.
又$k=\frac{{g({x_2})-g({x_1})}}{{{x_2}-{x_1}}}=\frac{{ln\frac{x_2}{x_1}}}{{{x_2}-{x_1}}}$,不妨设x2>x1,
要比较k与g'(x0)的大小,即比较$\frac{ln\frac{{x}_{2}}{{x}_{1}}}{\frac{{x}_{1}}{{x}_{2}-{x}_{1}}}$与$\frac{2}{{x}_{1}+{x}_{2}}$的大小,又因为x2>x1,
所以即比较ln$\frac{{x}_{2}}{{x}_{1}}$与$\frac{2({x}_{2}-{x}_{1})}{{x}_{2}+{x}_{1}}$=$\frac{2(\frac{{x}_{2}}{{x}_{1}}-1)}{\frac{{x}_{2}}{{x}_{1}}+1}$的大小.
令h(x)=lnx-$\frac{2(x-1)}{x+1},(x>1)$,则h′(x)=$\frac{(x-1)^{2}}{x(x+1)^{2}}≥0$,∴h(x)在[1,+∞)上是增函数.
又$\frac{{x}_{2}}{{x}_{1}}>1$,∴h($\frac{{x}_{2}}{{x}_{1}}$)>h(1)=0,∴$ln\frac{{x}_{2}}{{x}_{1}}>\frac{2(\frac{{x}_{2}}{{x}_{1}}-1)}{\frac{{x}_{2}}{{x}_{1}}+1}$,即k>g'(x0).…(14分)
点评 本题考查了导数的综合应用,考查了分类讨论思想、转化思想,属于难题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{5}$ |
| A. | ?x1,x2∈R,(f(x1)-f(x2))(x1-x2)>0 | B. | ?x1,x2∈R,(f(x1)-f(x2))(x1-x2)≥0 | ||
| C. | ?x1,x2∈R,(f(x1)-f(x2))(x1-x2)≥0 | D. | ?x1,x2∈R,(f(x1)-f(x2))(x1-x2)<0 |
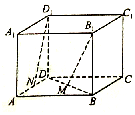 如图所示,在正方体ABCD-A1B1C1D1中,已知棱长为a,M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )
如图所示,在正方体ABCD-A1B1C1D1中,已知棱长为a,M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )| A. | $\frac{\sqrt{30}}{10}$ | B. | $\frac{\sqrt{30}}{10}$a | C. | -$\frac{\sqrt{30}}{10}$ | D. | $\frac{\sqrt{15}}{15}$a |