题目内容

1．若点（a，27）在函数y=x3的图象上，则tan$\frac{π}{a}$的值为$\sqrt{3}$．

分析 把点（a，27）代入y=x3，求出a的值，再计算tan$\frac{π}{a}$的值．

解答 解：把点（a，27）代入y=x3得，
a3=27，
解得a=3，
所以tan$\frac{π}{a}$=$\frac{π}{3}$=$\sqrt{3}$．
故答案为：$\sqrt{3}$．

点评 本题考查了幂函数的图象与性质的应用问题，也考查了求特殊角的正切值的应用问题，是基础题．

练习册系列答案
相关题目
11．给出下列命题：
①函数f（x）=$\frac{{\sqrt{|{x-2}|-1}}}{{{{log}_2}（x-1）}}$的定义域为[3，+∞）；
②将函数y=tanx图象上所有点的横坐标伸长到原来的2倍，纵坐标不变，再把图象向左平移$\frac{2π}{3}$个单位，得到g（x）的图象，则g（x）的单调递增区间是$（kπ-\frac{5π}{3}，kπ+\frac{π}{3}）（k∈Z）$；
③已知函数f（x）=$\left\{{\begin{array}{l}{{{10}^{-x}}-2，x≤0}\\{2ax-1，x＞0}\end{array}}$（a是常数且a＞0），若f（x）＞0在$[\frac{1}{2}，+∞）$上恒成立，则a的取值范围是[1，+∞）；
④已知函数f（x）=$\left\{{\begin{array}{l}{{{10}^{-x}}-2，x≤0}\\{2ax-1，x＞0}\end{array}}$（a是常数且a＞0），对任意的x1，x2＜0且x1≠x2，恒有$f（\frac{{{x_1}+{x_2}}}{2}）＜\frac{{f（{x_1}）+f（{x_2}）}}{2}$；
⑤已知函数f（x）=$\left\{{\begin{array}{l}{{x^3}，x≤a}\\{{x^2}，x＞a}\end{array}}$，若存在实数b，使函数g（x）=f（x）-b有两个零点，则a的取值范围是a＜0或a＞1．
其中正确命题的序号是①④⑤．（写出所有正确命题的序号）
12．已知i为虚数单位，复数$\frac{2+4i}{i}$=（　　）
A．4-2iB．4+2iC．-4-2iD．-4+2i
9．已知定义在R上的函数f（x）=|x-m|+|x|，m∈N*，存在实数x使f（x）＜2成立．
（Ⅰ）求实数m的值；
（Ⅱ）若α，β＞1，f（α）+f（β）=2，求证：$\frac{4}{α}$+$\frac{1}{β}$≥$\frac{9}{2}$．
16．已知集合A={0，1}，B={z|z=x+y，x∈A，y∈A}，则B的子集个数为（　　）
A．3B．4C．7D．8
6．在区间[-1，1]上随机取一个数k，使直线y=k（x+3）与圆x2+y2=1相交的概率为（　　）
A．$\frac{1}{2}$B．$\frac{1}{3}$C．$\frac{\sqrt{2}}{4}$D．$\frac{\sqrt{2}}{3}$
13．在△ABC中角A，B，C所对的边分别是a，b，c，b=$\sqrt{2}$，c=1，cosB=$\frac{3}{4}$．
（1）求sinC的值；
（2）求△ABC的面积．
10．设函数f（x）是定义在R上的偶函数，且对任意的x∈R，都有f（x+2）=f（x）．当-1≤x≤0时，f（x）=-x2，若直线y=-x+m与函数y=f（x）的图象有两个不同的公共点，则实数m的值为（　　）
A．2k-$\frac{1}{4}$（k∈Z）B．2k+$\frac{1}{4}$（k∈Z）C．2k或2k-$\frac{1}{4}$（k∈Z）D．2k或2k+$\frac{1}{4}$（k∈Z）
11．已知某几何体的三视图如图所示，则该几何体的表面积（　　）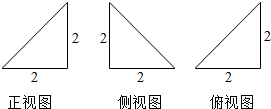
A．6B．$6+2\sqrt{3}$C．$8+8\sqrt{2}$D．$4+4\sqrt{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网