题目内容
11.给出下列命题:①函数f(x)=$\frac{{\sqrt{|{x-2}|-1}}}{{{{log}_2}(x-1)}}$的定义域为[3,+∞);
②将函数y=tanx图象上所有点的横坐标伸长到原来的2倍,纵坐标不变,再把图象向左平移$\frac{2π}{3}$个单位,得到g(x)的图象,则g(x)的单调递增区间是$(kπ-\frac{5π}{3},kπ+\frac{π}{3})(k∈Z)$;
③已知函数f(x)=$\left\{{\begin{array}{l}{{{10}^{-x}}-2,x≤0}\\{2ax-1,x>0}\end{array}}$(a是常数且a>0),若f(x)>0在$[\frac{1}{2},+∞)$上恒成立,则a的取值范围是[1,+∞);
④已知函数f(x)=$\left\{{\begin{array}{l}{{{10}^{-x}}-2,x≤0}\\{2ax-1,x>0}\end{array}}$(a是常数且a>0),对任意的x1,x2<0且x1≠x2,恒有$f(\frac{{{x_1}+{x_2}}}{2})<\frac{{f({x_1})+f({x_2})}}{2}$;
⑤已知函数f(x)=$\left\{{\begin{array}{l}{{x^3},x≤a}\\{{x^2},x>a}\end{array}}$,若存在实数b,使函数g(x)=f(x)-b有两个零点,则a的取值范围是a<0或a>1.
其中正确命题的序号是①④⑤.(写出所有正确命题的序号)
分析 ①根据函数成立的条件进行求解.
②根据三角函数的图象以及三角函数的单调性进行求解判断.
③根据函数恒成立,利用参数分离法进行求解.
④根据凹函数的性质,利用数形结合进行判断.
⑤由g(x)=f(x)-b有两个零点可得f(x)=b有两个零点,即y=f(x)与y=b的图象有两个交点,则函数在定义域内不能是单调函数,结合函数图象可求a的范围.
解答 解:①要使函数有意义,则$\left\{\begin{array}{l}{x-1>0}\\{lo{g}_{2}(x-1)≠0}\\{|x-2|-1≥0}\end{array}\right.$,即$\left\{\begin{array}{l}{x>1}\\{x≠2}\\{x≥3或x≤1}\end{array}\right.$,得x≥3,即函数的定义域为[3,+∞);故①正确,
②将函数y=tanx图象上所有点的横坐标伸长到原来的2倍,纵坐标不变,得到y=tan$\frac{1}{2}x$,
再把图象向左平移$\frac{2π}{3}$个单位,得到y=tan$\frac{1}{2}$(x+$\frac{2π}{3}$)=tan($\frac{1}{2}$x+$\frac{π}{3}$),即g(x)=tan($\frac{1}{2}$x+$\frac{π}{3}$),
由kπ-$\frac{π}{2}$<$\frac{1}{2}$x+$\frac{π}{3}$<kπ+$\frac{π}{2}$,k∈Z,得2kπ-$\frac{5π}{3}$<x<2kπ+$\frac{π}{3}$,k∈Z,即函数的单调递增区间为为(2kπ-$\frac{5π}{3}$,2kπ+$\frac{π}{3}$),k∈Z,故②错误,
③已知函数f(x)=$\left\{{\begin{array}{l}{{{10}^{-x}}-2,x≤0}\\{2ax-1,x>0}\end{array}}$(a是常数且a>0),
若f(x)>0在$[\frac{1}{2},+∞)$上恒成立,则2ax-1>0,即a>$\frac{1}{2x}$,
∵当x≥$\frac{1}{2}$时,$\frac{1}{2x}$≤$\frac{1}{2×\frac{1}{2}}$=1,则a>1,即a的取值范围是(1,+∞);故③错误,
④已知函数f(x)=$\left\{{\begin{array}{l}{{{10}^{-x}}-2,x≤0}\\{2ax-1,x>0}\end{array}}$(a是常数且a>0),对任意的x1,x2<0且x1≠x2,若$f(\frac{{{x_1}+{x_2}}}{2})<\frac{{f({x_1})+f({x_2})}}{2}$,则函数为凹函数,作出函数y=f(x)在x<0时的图象如图:
则函数为凹函数,满足条件.故④正确;
⑤解:∵g(x)=f(x)-b有两个零点,
∴f(x)=b有两个零点,即y=f(x)与y=b的图象有两个交点,
由x3=x2可得,x=0或x=1
当a>1时,函数f(x)的图象如图所示,此时存在b,满足题意,故a>1满足题意
当a=1时,由于函数f(x)在定义域R上单调递增,故不符合题意
当0<a<1时,函数f(x)单调递增,故不符合题意
④a=0时,f(x)单调递增,故不符合题意
⑤当a<0时,函数y=f(x)的图象如图所示,此时存在b使得,y=f(x)与y=b有两个交点
综上可得,a<0或a>1,故⑤正确,
故答案为:①④⑤
点评 本题主要考查命题的真假判断,涉及三角函数以及函数的性质,综合性较强,难度较大.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案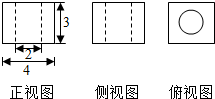 如图是一个空间几何体的三视图,其中正视图与侧视图完全一样,俯视图的外框为正方形,则这个几何体的表面积是( )
如图是一个空间几何体的三视图,其中正视图与侧视图完全一样,俯视图的外框为正方形,则这个几何体的表面积是( )| A. | 80-2π | B. | 80 | C. | 80+4π | D. | 80+6π |
| A. | 若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$|,则$\overrightarrow{a}$$⊥\overrightarrow{b}$ | B. | 若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$| | ||
| C. | 若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$|,则存在实数λ使得$\overrightarrow{a}$=$λ\overrightarrow{b}$ | D. | 若存在实数λ使得$\overrightarrow{a}$=$λ\overrightarrow{b}$,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$| |
| A. | “ac2>bc2”是“a>b”的充分不必要条件 | |
| B. | 若p∨q是假命题,则p∧q是假命题 | |
| C. | 命题“存在x0∈R,2${\;}^{{x}_{0}}$≤0”的否定是“对任意的x∈R,2x>0” | |
| D. | 命题“对任意的x∈R”,2x>x2”是真命题 |
 如图在正方体ABCD-A′B′C′D′中,
如图在正方体ABCD-A′B′C′D′中,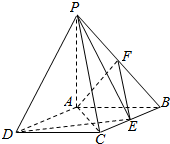 如图:四棱锥P-ABCD中,底面ABCD是平行四边形,且AC=BD,PA⊥底面ABCD,PA=AB=1,$BC=\sqrt{3}$,点F是PB的中点,点E在边BC上移动.
如图:四棱锥P-ABCD中,底面ABCD是平行四边形,且AC=BD,PA⊥底面ABCD,PA=AB=1,$BC=\sqrt{3}$,点F是PB的中点,点E在边BC上移动.