题目内容
9.已知定义在R上的函数f(x)=|x-m|+|x|,m∈N*,存在实数x使f(x)<2成立.(Ⅰ)求实数m的值;
(Ⅱ)若α,β>1,f(α)+f(β)=2,求证:$\frac{4}{α}$+$\frac{1}{β}$≥$\frac{9}{2}$.
分析 (I)|x-m|+|x|≥|x-m-x|=|m|,要使|x-m|+|x|<2有解,则|m|<2,m∈N*,解得m.
(II)α,β>1,f(α)+f(β)=2α-1+2β-1=2,可得α+β=2.再利用基本不等式的性质即可得出.
解答 (I)解:∵|x-m|+|x|≥|x-m-x|=|m|,
∴要使|x-m|+|x|<2有解,则|m|<2,解得-2<m<2.
∵m∈N*,∴m=1.
(II)证明:α,β>0,f(α)+f(β)=2α-1+2β-1=2,
∴α+β=2.
∴$\frac{4}{α}$+$\frac{1}{β}$=$\frac{1}{2}(α+β)$$(\frac{4}{α}+\frac{1}{β})$=$\frac{1}{2}(5+\frac{4β}{α}+\frac{α}{β})$≥$\frac{1}{2}(5+2\sqrt{\frac{4β}{α}•\frac{α}{β}})$=$\frac{9}{2}$,当且仅当α=2β=$\frac{4}{3}$时取等号.
点评 本题考查了绝对值不等式的性质、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
19.设$\overrightarrow{a}$,$\overrightarrow{b}$是两个非零向量,则下列哪个描述是正确的( )
| A. | 若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$|,则$\overrightarrow{a}$$⊥\overrightarrow{b}$ | B. | 若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$| | ||
| C. | 若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$|,则存在实数λ使得$\overrightarrow{a}$=$λ\overrightarrow{b}$ | D. | 若存在实数λ使得$\overrightarrow{a}$=$λ\overrightarrow{b}$,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$| |
20.已知等比数列{an}中,各项都是正数,且3a1,$\frac{1}{2}{a_3}$,2a2成等差数列,则$\frac{{{a_8}+{a_9}}}{{{a_6}+{a_7}}}$等于( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
4.已知f(x)在R上是奇函数,且满足f(x+4)=f(x),当x∈(0,2)时,f(x)=2x2,则f(7)=( )
| A. | 2 | B. | -2 | C. | -98 | D. | 98 |
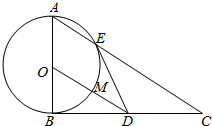 如图,在△ABC中,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.
如图,在△ABC中,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.