题目内容
11.已知某几何体的三视图如图所示,则该几何体的表面积( )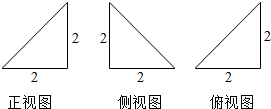
| A. | 6 | B. | $6+2\sqrt{3}$ | C. | $8+8\sqrt{2}$ | D. | $4+4\sqrt{2}$ |
分析 根据已知的三视图,得出该几何体是一个以俯视图为底面的直三棱锥,画出图形,求出它的表面积即可.
解答 解:由已知的三视图得:该几何体是一个以俯视图为底面的直三棱锥,
如图所示:
其四个顶点是以俯视图为底面,以2为高的三棱柱的四个顶点,
所以该三棱锥的表面积为
S=S△ABC+S△PAB+S△PBC+S△PAC
=$\frac{1}{2}$×2×2+$\frac{1}{2}$×2×2$\sqrt{2}$+$\frac{1}{2}$×2×2+$\frac{1}{2}$×2×2$\sqrt{2}$
=4+4$\sqrt{2}$.
故选:D.
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.如图所示,网格纸上小正方形的边长为1cm,粗实线为某空间几何体的三视图,则该几何体的体积为( ) 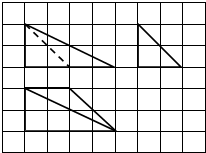

| A. | 2 cm3 | B. | 4 cm3 | C. | 6 cm3 | D. | 8 cm3 |
3.已知圆C:(x-1)2+(y-2)2=2截y轴所得线段与截直线y=2x+b所得线段的长度相等,则b=( )
| A. | $-\sqrt{6}$ | B. | ±$\sqrt{6}$ | C. | $-\sqrt{5}$ | D. | ±$\sqrt{5}$ |
20.已知点(x,y)满足(x-1)2+(y-1)2≤1,则满足(y-x)(y-$\frac{1}{x}$)≥0的概率为( )
| A. | $\frac{π}{2}$ | B. | $\frac{4}{7}$π | C. | $\frac{1}{2}$ | D. | $\frac{4}{7}$ |
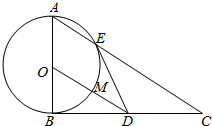 如图,在△ABC中,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.
如图,在△ABC中,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.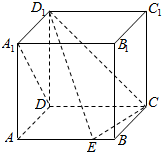 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱AB上的动点.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱AB上的动点.