题目内容
某地区的绿化面积每年平均比上一年增长10%,设经过x年后,绿化面积与原绿化面积之比为y,则y=f(x)得图象大致为( )
A、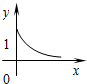 |
B、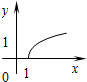 |
C、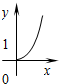 |
D、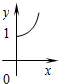 |
考点:函数的图象
专题:函数的性质及应用
分析:依题意,先表示出y的解析式,可得到绿化面积与原绿化面积之比的解析式,利用函数的性质即可得到答案.
解答:
解:设某地区起始年的绿化面积为t,
∵该地区的绿化面积每年平均比上一年增长10%,
∴经过x年,绿化面积g(x)=t(1+10%)x,
∵绿化面积与原绿化面积之比为y,则y=f(x)=
=(1+10%)x=1.1x,
∵y=1.1x为底数大于1的指数函数,
只有D符合
故选:D.
∵该地区的绿化面积每年平均比上一年增长10%,
∴经过x年,绿化面积g(x)=t(1+10%)x,
∵绿化面积与原绿化面积之比为y,则y=f(x)=
| g(x) |
| t |
∵y=1.1x为底数大于1的指数函数,
只有D符合
故选:D.
点评:本题考查函数的图象与性质,利用函数性质来识图,着重考查指数函数的性质,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
点A(2,0),B(4,2),若|
|=2|
|,则点C坐标为( )
| AB |
| AC |
| A、(1,-1) |
| B、(1,-1)或(5,-1) |
| C、(1,-1)或(3,1) |
| D、无数多个 |
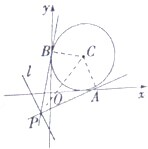 已知P是直线l:3x+4y+8=0上的动点,PA,PB是圆C:x2+y2-2x-2y+1=0的两条切线,A、B是切点.
已知P是直线l:3x+4y+8=0上的动点,PA,PB是圆C:x2+y2-2x-2y+1=0的两条切线,A、B是切点.