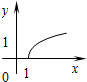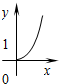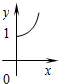题目内容
点A(2,0),B(4,2),若|
|=2|
|,则点C坐标为( )
| AB |
| AC |
| A、(1,-1) |
| B、(1,-1)或(5,-1) |
| C、(1,-1)或(3,1) |
| D、无数多个 |
考点:轨迹方程,平面向量的正交分解及坐标表示
专题:平面向量及应用
分析:在直角坐标系中画出图形,判断选项即可.
解答:
 解:点A(2,0),B(4,2),若|
解:点A(2,0),B(4,2),若|
|=2|
|,如图:
显然C的坐标是圆周上的点,有无数个.
故选:D.
 解:点A(2,0),B(4,2),若|
解:点A(2,0),B(4,2),若|| AB |
| AC |
显然C的坐标是圆周上的点,有无数个.
故选:D.
点评:本题考查向量的模的求法,轨迹方程的应用,考查分析问题解决问题的能力.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
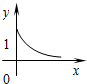
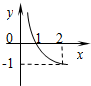 已知函数f(x)=logax(a>0,且a≠1)的图象如图所示,函数y=g(x)是函数y=f(x)的反函数,则函数y=g(x)的解析式为( )
已知函数f(x)=logax(a>0,且a≠1)的图象如图所示,函数y=g(x)是函数y=f(x)的反函数,则函数y=g(x)的解析式为( )| A、g(x)=2x | ||
B、g(x)=(
| ||
C、g(x)=log
| ||
| D、g(x)=log2x |
若a,b∈R,则下列命题正确的是( )
| A、若a>b,则a2>b2 | ||||
B、若a>b,则
| ||||
| C、若a>|b|,则a2>b2 | ||||
| D、若ac>bc,则a>b |
函数y=
x4-x3的极值点的个数为( )
| 3 |
| 4 |
| A、0个 | B、1个 | C、2个 | D、3个 |
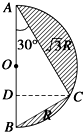 如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,∠BAC=30°,则此几何体的体积为
如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,∠BAC=30°,则此几何体的体积为