题目内容
函数f（x）=
的定义域是 ．
| ax+b |
| cx+d |
考点：函数的定义域及其求法
专题：计算题,函数的性质及应用
分析：由题意，cx+d≠0，注意讨论c是否为0．
解答：
解：由题意，
cx+d≠0，
若c=0，则d≠0，其定义域为R；
若c≠0，则x≠-
，
其定义域为：{x|x≠-
}．
故答案为：R（c=0）或{x|x≠-
}（c≠0）．
cx+d≠0，
若c=0，则d≠0，其定义域为R；
若c≠0，则x≠-
| d |
| c |
其定义域为：{x|x≠-
| d |
| c |
故答案为：R（c=0）或{x|x≠-
| d |
| c |
点评：本题考查了函数的定义域的求法，由题意知分母不能为0，注意讨论即可，属于基础题．
练习册系列答案
金钥匙试卷系列答案
相关题目
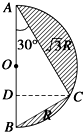如图所示，半径为R的半圆内的阴影部分以直径AB所在直线为轴，旋转一周得到一几何体，∠BAC=30°，则此几何体的体积为
