题目内容
已知
=(1,k),
=(4,2),|
|≤5,k∈Z,则△ABC是钝角三角形的概率为( )
| AB |
| AC |
| AB |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:本题考查的知识点是古典概型,我们根据|
|≤5,及k∈Z易求出满足条件的所有的k,然后分类讨论△ABC是钝角三角形时k的取值情况,然后代入古典概型计算公式,即可得到答案.
| AB |
解答:
解:∵|
|=
≤5,
∴-2
≤k≤2
,
∵k∈Z,
∴k=0,±1,±2,±3,±4,
∵
=
-
=(3,2-k),
若
•
<0,则k<-2,∴k=-3,-4,
若
•
<0,则-1<k<3,∴k=0,1,2,
若
•
<0,则k>8,(舍去),
∴△ABC是钝角三角形的概率P=
,
故选:C
| AB |
| 1+k2 |
∴-2
| 6 |
| 6 |
∵k∈Z,
∴k=0,±1,±2,±3,±4,
∵
| BC |
| AC |
| AB |
若
| AB |
| AC |
若
| BA |
| BC |
若
| CA |
| CB |
∴△ABC是钝角三角形的概率P=
| 5 |
| 9 |
故选:C
点评:古典概型要求所有结果出现的可能性都相等,强调所有结果中每一结果出现的概率都相同.弄清一次试验的意义以及每个基本事件的含义是解决问题的前提,正确把握各个事件的相互关系是解决问题的关键.解决问题的步骤是:计算满足条件的基本事件个数,及基本事件的总个数,然后代入古典概型计算公式进行求解

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
函数y=
的图象大致是( )
| log2|x| |
| x |
A、 |
B、 |
C、 |
D、 |
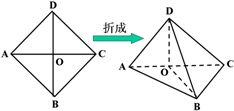 如图,以正方形ABCD的对角线AC为折痕,使△ADC和△ABC折成相垂直的两个面,点O为AC的中点.
如图,以正方形ABCD的对角线AC为折痕,使△ADC和△ABC折成相垂直的两个面,点O为AC的中点.