题目内容
已知函数f(x)=
,则方程f(x)=ax恰有两个不同的实根时,实数a的取值范围是 .
|
考点:分段函数的应用
专题:计算题,作图题,函数的性质及应用
分析:由题意,方程f(x)=ax恰有两个不同实数根,等价于y=f(x)与y=ax有2个交点,又a表示直线y=ax的斜率,作出图象从而求出a的取值范围.
解答:
 解:∵方程f(x)=ax恰有两个不同实数根,
解:∵方程f(x)=ax恰有两个不同实数根,
∴y=f(x)与y=ax有2个交点,a表示直线y=ax的斜率,
作函数f(x)=
的图象如右图,
当x>1时,f′(x)=
,
设切点为(x0,y0),k=
,
∴切线方程为y-y0=
(x-x0),而切线过原点,
∴y0=1,x0=e,k=
,
∴直线l1的斜率为
,
又∵直线l2与y=
x+1平行,
∴直线l2的斜率为
,
∴实数a的取值范围是[
,
),
故答案为:[
,
).
 解:∵方程f(x)=ax恰有两个不同实数根,
解:∵方程f(x)=ax恰有两个不同实数根,∴y=f(x)与y=ax有2个交点,a表示直线y=ax的斜率,
作函数f(x)=
|
当x>1时,f′(x)=
| 1 |
| x |
设切点为(x0,y0),k=
| 1 |
| x0 |
∴切线方程为y-y0=
| 1 |
| x0 |
∴y0=1,x0=e,k=
| 1 |
| e |
∴直线l1的斜率为
| 1 |
| e |
又∵直线l2与y=
| 1 |
| 6 |
∴直线l2的斜率为
| 1 |
| 6 |
∴实数a的取值范围是[
| 1 |
| 6 |
| 1 |
| e |
故答案为:[
| 1 |
| 6 |
| 1 |
| e |
点评:本题考查了分段函数的图象的作法,同时考查了数形结合的数学思想的应用,属于难题.

练习册系列答案
相关题目
已知函数f(x)=sin(
x+θ)-
cos(
x+θ)(|θ|<
)的图象关于y轴对称,则y=f(x)在下列哪个区间上是减函数( )
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| π |
| 2 |
A、(0,
| ||||
B、(-
| ||||
C、(
| ||||
D、(
|
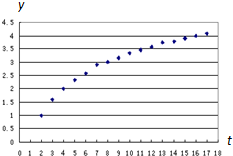 某研究小组在一项实验中获得一组关于y、t之间的数据,将其整理后得到如图所示的散点图,下列函数中,最能近似刻画y与t之间关系的是( )
某研究小组在一项实验中获得一组关于y、t之间的数据,将其整理后得到如图所示的散点图,下列函数中,最能近似刻画y与t之间关系的是( )| A、y=2t |
| B、y=2t2 |
| C、y=log2t |
| D、y=t3 |
数列{an}的通项为an=(-1)n•n•sin
+1前n项和为Sn,S100=( )
| nπ |
| 2 |
| A、50 | B、100 |
| C、-150 | D、150 |
已知
=(1,k),
=(4,2),|
|≤5,k∈Z,则△ABC是钝角三角形的概率为( )
| AB |
| AC |
| AB |
A、
| ||
B、
| ||
C、
| ||
D、
|
直线x+y-2=0与圆(x-1)2+(y-2)2=1相交于A,B两点,则弦|AB|=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|