题目内容
如果正四棱锥的对角线和侧面所形成的角为30°,底面边长为a,则它的体积是 .
考点:直线与平面所成的角
专题:计算题,作图题,空间位置关系与距离
分析:作图如下,取AB的中点E,连结OE、SE,作OF⊥SE于点F,连结BF,可证明∠FBO=30°,从而可得OF=
a,从而可求得∠SEO=45°,则SO=OE=
,从而求得其体积.
| ||
| 4 |
| a |
| 2 |
解答:
 解:作图如右图,
解:作图如右图,
取AB的中点E,连结OE、SE,
作OF⊥SE于点F,连结BF,
∵SO⊥AB,OE⊥AB,
∴AB⊥平面SOE,
又∵OF?平面SOE,
∴AB⊥OF,
又∵OF⊥SE,
∴OF⊥平面SAB,
则∠FBO=30°,
∴OF=
OB=
×
a=
a,
在Rt△FOE中,又∵OE=
,
故∠SEO=45°,
故SO=OE=
,
故其体积为V=
×a2×
×a=
.
故答案为:
.
 解:作图如右图,
解:作图如右图,取AB的中点E,连结OE、SE,
作OF⊥SE于点F,连结BF,
∵SO⊥AB,OE⊥AB,
∴AB⊥平面SOE,
又∵OF?平面SOE,
∴AB⊥OF,
又∵OF⊥SE,
∴OF⊥平面SAB,
则∠FBO=30°,
∴OF=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
在Rt△FOE中,又∵OE=
| a |
| 2 |
故∠SEO=45°,
故SO=OE=
| a |
| 2 |
故其体积为V=
| 1 |
| 3 |
| 1 |
| 2 |
| a3 |
| 6 |
故答案为:
| a3 |
| 6 |
点评:本题考查了学生的作图能力及体积的求法,属于中档题.

练习册系列答案
相关题目
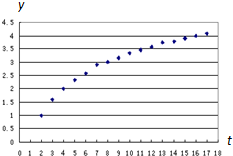 某研究小组在一项实验中获得一组关于y、t之间的数据,将其整理后得到如图所示的散点图,下列函数中,最能近似刻画y与t之间关系的是( )
某研究小组在一项实验中获得一组关于y、t之间的数据,将其整理后得到如图所示的散点图,下列函数中,最能近似刻画y与t之间关系的是( )| A、y=2t |
| B、y=2t2 |
| C、y=log2t |
| D、y=t3 |
数列{an}的通项为an=(-1)n•n•sin
+1前n项和为Sn,S100=( )
| nπ |
| 2 |
| A、50 | B、100 |
| C、-150 | D、150 |
已知
=(1,k),
=(4,2),|
|≤5,k∈Z,则△ABC是钝角三角形的概率为( )
| AB |
| AC |
| AB |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知数列{an}满足a1=1,an+1-
=1,则a6-a5的值为( )
| 1 |
| an |
| A、0 | ||
| B、1 | ||
C、
| ||
D、
|