题目内容
函数y=
的图象大致是（ ）
| log2|x| |
| x |
A、 |
B、 |
C、 |
D、 |
考点：函数的图象
专题：常规题型,函数的性质及应用
分析：观察选项中图象的不同，选择函数的性质，从而用排除法解答．
解答：
解：∵f（-x）=
=-f（x），
∴函数y=
的图象关于原点对称，
故排除B，
当x→+∞时，y→0，且为正值，故排除A、D，
故选C．
| log2|-x| |
| -x |
∴函数y=
| log2|x| |
| x |
故排除B，
当x→+∞时，y→0，且为正值，故排除A、D，
故选C．
点评：本题考查了函数的图象的判断，常利用排除法．
练习册系列答案
相关题目
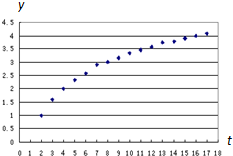某研究小组在一项实验中获得一组关于y、t之间的数据，将其整理后得到如图所示的散点图，下列函数中，最能近似刻画y与t之间关系的是（ ）| A、y=2t |
| B、y=2t2 |
| C、y=log2t |
| D、y=t3 |
已知
=（1，k），
=（4，2），|
|≤5，k∈Z，则△ABC是钝角三角形的概率为（ ）
| AB |
| AC |
| AB |
A、
| ||
B、
| ||
C、
| ||
D、
|
直线x+y-2=0与圆（x-1）2+（y-2）2=1相交于A，B两点，则弦|AB|=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
对实数a和b，定义运算“*”：a*b=
，设函数f（x）=（x2+1）*（x+2），若函数y=f（x）-c的图象与x轴恰有两个公共点，则实数c的取值范围是（ ）
|
| A、（1，2]∪（4，5] |
| B、（2，4]∪（5，+∞） |
| C、（-∞，1）∪（4，5] |
| D、[1，2] |
已知数列{an}满足a1=1，an+1-
=1，则a6-a5的值为（ ）
| 1 |
| an |
| A、0 | ||
| B、1 | ||
C、
| ||
D、
|
设集合P={a2，log2a}，Q={2a，b}，若P∩Q={0}，则P∪Q=（ ）
| A、{0，1} |
| B、{0，1，2} |
| C、{0，2} |
| D、{0，1，2，3} |