题目内容
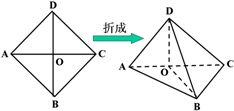 如图,以正方形ABCD的对角线AC为折痕,使△ADC和△ABC折成相垂直的两个面,点O为AC的中点.
如图,以正方形ABCD的对角线AC为折痕,使△ADC和△ABC折成相垂直的两个面,点O为AC的中点.(1)求证:DO⊥OB;
(2)求BD与平面ABC所成的角.
考点:直线与平面所成的角,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(1)由二面角的定义和面面垂直可得;
(2)由线面角的定义可知∠DBO为BD与平面ABC所成的角,由等腰直角三角形易得.
(2)由线面角的定义可知∠DBO为BD与平面ABC所成的角,由等腰直角三角形易得.
解答:
解:(1)由题意△ADC和△ABC为互相垂直的两个面,
∵点O为AC的中点,∴OB⊥AC且OD⊥AC,
∴∠DOB即为二面角D-AC-B的平面角,
∴∠DOB为90°,∴DO⊥OB;
(2)由(1)知,OB为DB在平面ABC的射影直线,
∴∠DBO为BD与平面ABC所成的角,
在RT△DBO中,OB=OD,∴∠DBO=45°
∴BD与平面ABC所成的角为45°
∵点O为AC的中点,∴OB⊥AC且OD⊥AC,
∴∠DOB即为二面角D-AC-B的平面角,
∴∠DOB为90°,∴DO⊥OB;
(2)由(1)知,OB为DB在平面ABC的射影直线,
∴∠DBO为BD与平面ABC所成的角,
在RT△DBO中,OB=OD,∴∠DBO=45°
∴BD与平面ABC所成的角为45°
点评:本题考查直线与平面所成的角和二面角,找到所成的角是解决问题的关键,属中档题.

练习册系列答案
相关题目
已知函数f(x)=sin(
x+θ)-
cos(
x+θ)(|θ|<
)的图象关于y轴对称,则y=f(x)在下列哪个区间上是减函数( )
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| π |
| 2 |
A、(0,
| ||||
B、(-
| ||||
C、(
| ||||
D、(
|
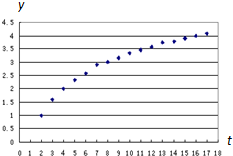 某研究小组在一项实验中获得一组关于y、t之间的数据,将其整理后得到如图所示的散点图,下列函数中,最能近似刻画y与t之间关系的是( )
某研究小组在一项实验中获得一组关于y、t之间的数据,将其整理后得到如图所示的散点图,下列函数中,最能近似刻画y与t之间关系的是( )| A、y=2t |
| B、y=2t2 |
| C、y=log2t |
| D、y=t3 |
已知
=(1,k),
=(4,2),|
|≤5,k∈Z,则△ABC是钝角三角形的概率为( )
| AB |
| AC |
| AB |
A、
| ||
B、
| ||
C、
| ||
D、
|