题目内容
已知向量
=(2,1),
=(x,y).若x∈[-1,2],y∈[-1,1],则向量
,
的夹角是钝角的概率是 .
| a |
| b |
| a |
| b |
考点:几何概型
专题:概率与统计
分析:本题是一个等可能事件的概率,试验发生包含的事件和满足条件的事件可以利用集合来表示,做出集合对应的面积,利用面积之比得到概率.
解答:
 解:设“
解:设“
,
的夹角是钝角”为事件B,由
,
的夹角是钝角,可得
•
<0,即2x+y<0,且x≠2y.基本事件空间为Ω={,(x,y)|,
,}
B={,(x,y)|,
,},则P(B)=
=
=
,
即向量
,
的夹角是钝角的概率是
.
故答案为:
 解:设“
解:设“| a |
| b |
| a |
| b |
| a |
| b |
|
B={,(x,y)|,
|
| uB |
| uΩ |
| ||||||
| 2×3 |
| 1 |
| 3 |
即向量
| a |
| b |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积、和体积、的比值得到.

练习册系列答案
相关题目
任取实数a、b∈[-1,1],则a、b满足|a-2b|≤2的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
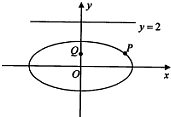 已知椭圆C:
已知椭圆C: