Question

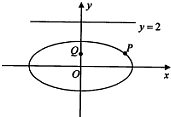已知椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0），经过点P（

3

，

1

2

），离心率e=

3

2

．
（1）求椭圆C的标准方程．
（2）过点Q（0，

1

2

）的直线与椭圆交于A、B两点，与直线y=2交于点M（直线AB不经过P点），记PA、PB、PM的斜率分别为k₁、k₂、k₃，问：是否存在常数λ，使得

1

k1

+

1

k2

=

λ

k3

？若存在，求出λ的值：若不存在，请说明理由．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（1）由已知条件设椭圆C的方程为

x2

4b2

+

y2

b2

=1，再由椭圆经过点P（

3

，

1

2

），能求出椭圆C的标准方程．
（2）当直线AB斜率不存在时，有

1

k1

+

1

k2

=

2

k3

，λ=2；当直线AB斜率k存在时，设A（x₁，y₁），B（x₂，y₂），设直线AB：y=kx+

1

2

，则M(

3

2k

，2)，联立

y=kx+ 1 2 x2 4 +y2=1

，得（1+4k²）x²+4kx-3=0，利用韦达定理结合题设条件能推导出

1

k1

+

1

k2

=

2

k3

，故存在常数λ=2符合题意．

解答： 解：（1）∵椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0），离心率e=

3

2

，
∴

c

a

=

3

2

，

c2

a2

=

a2-b2

a2

=1-

b2

a2

=

3

4

，
∴a²=4b²，∴椭圆方程为

x2

4b2

+

y2

b2

=1，
∵椭圆经过点P（

3

，

1

2

），∴

3

4b2

+

1

4b2

=1，
解得b²=1，∴椭圆C的标准方程

x2

4

+y2=1．…（4分）
（2）当直线AB斜率不存在时，
A(0，-1)，B(0，1)，P(

3

，

1

2

)，有

1

k1

+

1

k2

=

2

k3

，∴λ=2，…（5分）
当直线AB斜率k存在时，
由已知有k≠0，设A（x₁，y₁），B（x₂，y₂），
设直线AB：y=kx+

1

2

，则M(

3

2k

，2)，…（6分）
联立

y=kx+ 1 2 x2 4 +y2=1

，得（1+4k²）x²+4kx-3=0，
∴

x1+x2= -4k 1+4k2 x1x2= -3 1+4k2

…（7分）
∴

1

k1

+

1

k2

=

x1- 3

y1- 1 2

+

x2- 3

y2- 1 2

=

x1- 3

kx1

+

x2- 3

kx2

=

1

k

[

x1- 3

x1

+

x2- 3

x2

]
=

1

k

2x1x2- 3 (x1+x2)

x1x2

=

2

k

-

4 3

3

，…（10分）
∵

1

k3

=

3 2k - 3

2- 1 2

=

1

k

-

2 3

3

…（12分）
∴

1

k1

+

1

k2

=

2

k3

，∴λ=2，故存在常数λ=2符合题意．…（13分）

点评：本题考查椭圆的标准方程的求法，考查满足条件的实数值的求法，解题时要认真审题，注意函数与方程思想的合理运用．