题目内容
1.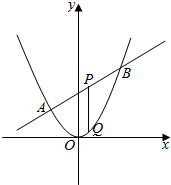 已知抛物线C:x2=2py(p>0)的焦点为F,直线2x-y+2=0交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.
已知抛物线C:x2=2py(p>0)的焦点为F,直线2x-y+2=0交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.(1)若直线AB过焦点F,求|AF|•|BF|的值;
(2)是否存在实数p,使得以线段AB为直径的圆过Q点?若存在,求出p的值;若不存在,说明理由.
分析 (1)求出p=4,可得抛物线方程,与直线y=2x+2联立消去y,设A(x1,y1),B(x2,y2),利用韦达定理,通过|AF||BF|=(y1+2)(y2+2)求解即可.
(2)假设存在,由抛物线x2=2py与直线y=2x+2联立消去y,设A(x1,y1),B(x2,y2),通过△>0,以及韦达定理推出P(2p,4p+2),Q(2p,2p),
方法一利用弦长公式$且|{PQ}|=\frac{1}{2}|{AB}|$,求出p.
方法二:通过$\overrightarrow{QA}•\overrightarrow{QB}=0$化简,结合韦达定理,求解p即可.
解答 解:(1)∵F(0,2),p=4,∴抛物线方程为x2=8y,…(1分)
与直线y=2x+2联立消去y得:x2-16x-16=0,设A(x1,y1),B(x2,y2)…(2分)
则x1+x2=16,x1x2=-16,…(3分)
∴|AF||BF|=(y1+2)(y2+2)=(2x1+4)(2x2+4)=80;…(6分)
(2)假设存在,由抛物线x2=2py与直线y=2x+2联立消去y得:x2-4px-4p=0.
设A(x1,y1),B(x2,y2),△>0,则x1+x2=4p,x1x2=-4p,…(7分)
P(2p,4p+2),Q(2p,2p),…(8分)
方法一∴|PQ|=2p+2,…(9分)
$又∵|{AB}|=\sqrt{5}•\sqrt{{{(4p)}^2}+16p}=4\sqrt{5}•\sqrt{{p^2}+p}$…(10分)
$且|{PQ}|=\frac{1}{2}|{AB}|$,
∴4p2+3p-1=0,
$p=\frac{1}{4}或p=-1(舍)$…(11分)
故存在p=$\frac{1}{4}$且满足△>0…(12分)
方法二:由$\overrightarrow{QA}•\overrightarrow{QB}=0$得:(x1-2p)(x2-2p)+(y1-2p)(y2-2p)=0…(9分)
即(x1-2p)(x2-2p)+(2x1+2-2p)(x2+2-2p)=0,…(10分)
∴$5{x_1}{x_2}+(4-6p)({x_1}+{x_2})+8{p^2}-8p+4=0$,…(11分)
代入得4p2+3p-1=0,$p=\frac{1}{4}或p=-1(舍)$.
故存在p=$\frac{1}{4}$且满足△>0,
∴p=$\frac{1}{4}$ …(12分)
点评 本题考查抛物线的简单性质以及直线与圆锥曲线的综合应用,考查转化思想以及计算能力.

 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
| A. | 19π | B. | 38π | C. | 48π | D. | $\frac{{19\sqrt{38}}}{3}π$ |

| A. | 24 | B. | 36 | C. | 72 | D. | 144 |
| 参加纪念活动的环节数 | 0 | 1 | 2 | 3 |
| 概率 | $\frac{1}{6}$ | m | n | $\frac{1}{3}$ |
(Ⅱ)某医疗部门决定从(1)中抽取的6名抗战老兵中随机抽取2名进行体检,求这2名抗战老兵中至少有1人参加纪念活动的环节数为3的概率.
| A. | $\frac{3}{π}$ | B. | $\frac{{3\sqrt{3}}}{4π}$ | C. | $\frac{{\sqrt{3}}}{4π}$ | D. | $\frac{{2\sqrt{3}}}{3π}$ |
 一个如图所示的密闭容器,它的下部是一个底面半径为1m,高为2m的圆锥体,上半部是个半球,则这个密闭容器的表面积是多少?体积为多少?
一个如图所示的密闭容器,它的下部是一个底面半径为1m,高为2m的圆锥体,上半部是个半球,则这个密闭容器的表面积是多少?体积为多少?