题目内容
11.一个圆内有一个内接等边三角形,一动点在圆内运动,则此点落在等边三角形内部的概率为( )| A. | $\frac{3}{π}$ | B. | $\frac{{3\sqrt{3}}}{4π}$ | C. | $\frac{{\sqrt{3}}}{4π}$ | D. | $\frac{{2\sqrt{3}}}{3π}$ |
分析 根据几何概型的概率公式求出对应的面积进行计算即可.
解答  解:设圆的半径为R,则圆内接等边三角形的边长为$\sqrt{3}$R,
解:设圆的半径为R,则圆内接等边三角形的边长为$\sqrt{3}$R,
则正三角形的面积S=$\frac{1}{2}$×($\sqrt{3}$R)2×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{4}$R2,
圆的面积S=πR2,
则点落在等边三角形内部的概率为P=$\frac{\frac{3\sqrt{3}}{4}{R}^{2}}{π{R}^{2}}$=$\frac{{3\sqrt{3}}}{4π}$,
故选:B.
点评 本题主要考查几何概型的概率的计算,根据条件求出对应的面积是解决本题的关键.

练习册系列答案
相关题目
19.运行如图所示的程序,最后输出的结果是( )


| A. | 3 | B. | 1 | C. | c=3 | D. | c=1 |
3.若$\overrightarrow a=({2sin2x,-1}),\overrightarrow b=({{{sin}^2}x,sin2x})$,且函数$f(x)=\overrightarrow a•\overrightarrow b$,则f(x)是( )
| A. | 最小正周期为$\frac{π}{2}$的奇函数 | B. | 最小正周期为π的奇函数 | ||
| C. | 最小正周期为$\frac{π}{2}$的偶函数 | D. | 最小正周期为π的偶函数 |
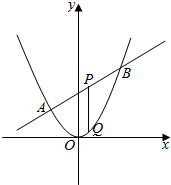 已知抛物线C:x2=2py(p>0)的焦点为F,直线2x-y+2=0交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.
已知抛物线C:x2=2py(p>0)的焦点为F,直线2x-y+2=0交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.