题目内容
12.设函数f(x)=$\sqrt{2x-5}$的定义域为A,B={x|x2≥a2}.(1)若a=2,求A∩B;
(2)若A⊆B,求实数a的取值范围.
分析 根据函数解析式有意义的原则可以求出集合A,
(1)将a=2代入集合B,结合集合交集运算法则可得答案.
(2)根据B={x|x≤-|a|或x≥|a|},要使A⊆B,需要|a|≤$\frac{5}{2}$,可得实数a的取值范围.
解答 解:函数f(x)=$\sqrt{2x-5}$的定义域A={x|x>$\frac{5}{2}$},
(1)当a=2时,B={x|x≤-2或x≥2}
此时A∩B={x|x>$\frac{5}{2}$}
(2)B={x|x≤-|a|或x≥|a|},
要使A⊆B,需要|a|≤$\frac{5}{2}$,即-$\frac{5}{2}$≤a≤$\frac{5}{2}$.
点评 本题考查的知识点是函数的定义域,函数的值域,集合的交集、并集运算,其中求出集合A,B是解答的关键.

练习册系列答案
相关题目
3.点A是椭圆$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>1)的上顶点,B、C是该椭圆的另外两点,且△ABC是以点A为直角顶点的等腰直角三角形,若满足条件的△ABC只有一个,则椭圆的离心率e的范围是( )
| A. | $\frac{\sqrt{3}}{3}$≤e<1 | B. | 0<e≤$\frac{\sqrt{3}}{3}$ | C. | 0<e≤$\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{3}$≤e<1 |
20.抛物线y=$\frac{1}{2}$x2的焦点坐标是( )
| A. | (0,$\frac{1}{8}$) | B. | (-$\frac{1}{8}$,0) | C. | (-$\frac{1}{2}$,0) | D. | (0,$\frac{1}{2}$) |
4.若等差数列{an}的前7项和S7=21,且a2=-1,则a6=( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
 在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别为A1D1和A1B1的中点.
在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别为A1D1和A1B1的中点.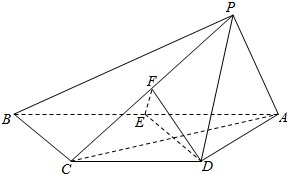 如图,四棱锥P-ABCD中,AP⊥平面PBC,AB∥DC,AP=AD=DC=$\frac{1}{2}$AB=1,∠ADC=120°,E,F分别为线段AB,PC的中点.
如图,四棱锥P-ABCD中,AP⊥平面PBC,AB∥DC,AP=AD=DC=$\frac{1}{2}$AB=1,∠ADC=120°,E,F分别为线段AB,PC的中点.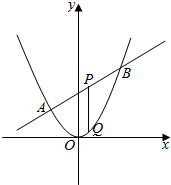 已知抛物线C:x2=2py(p>0)的焦点为F,直线2x-y+2=0交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.
已知抛物线C:x2=2py(p>0)的焦点为F,直线2x-y+2=0交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.