题目内容
13.如图是某几何体的三视图,则该几何体的体积为( )
| A. | 24 | B. | 36 | C. | 72 | D. | 144 |
分析 由已知中的三视图可得:该几何体是一个以俯视图为底面的四棱柱,代入柱体体积公式,可得答案.
解答 解:由已知中的三视图可得:该几何体是一个以俯视图为底面的四棱柱,
其底面面积S=$\frac{1}{2}$×(2+4)×3=9,
高h=8,
故体积V=Sh=72,
故选:C
点评 本题考查的知识点是由三视图,求体积和表面积,根据已知的三视图,判断几何体的形状是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.点A是椭圆$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>1)的上顶点,B、C是该椭圆的另外两点,且△ABC是以点A为直角顶点的等腰直角三角形,若满足条件的△ABC只有一个,则椭圆的离心率e的范围是( )
| A. | $\frac{\sqrt{3}}{3}$≤e<1 | B. | 0<e≤$\frac{\sqrt{3}}{3}$ | C. | 0<e≤$\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{3}$≤e<1 |
4.若等差数列{an}的前7项和S7=21,且a2=-1,则a6=( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
18.如图,当输入x=-5,y=15时,图中程序运行后输出的结果为( )


| A. | 3;33 | B. | 33;3 | C. | -17;7 | D. | 7;-17 |
5.若loga2<logb2<0,则a,b满足的关系是( )
| A. | 1<a<b | B. | 1<b<a | C. | 0<a<b<1 | D. | 0<b<a<1 |
3.若$\overrightarrow a=({2sin2x,-1}),\overrightarrow b=({{{sin}^2}x,sin2x})$,且函数$f(x)=\overrightarrow a•\overrightarrow b$,则f(x)是( )
| A. | 最小正周期为$\frac{π}{2}$的奇函数 | B. | 最小正周期为π的奇函数 | ||
| C. | 最小正周期为$\frac{π}{2}$的偶函数 | D. | 最小正周期为π的偶函数 |
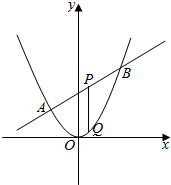 已知抛物线C:x2=2py(p>0)的焦点为F,直线2x-y+2=0交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.
已知抛物线C:x2=2py(p>0)的焦点为F,直线2x-y+2=0交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.