题目内容
(参考公式:[ln(1+x)]′=
)设函数f(x)=x-
(1)令N(x)=(1+x)2-1+ln(1+x),判断并证明N(x)在(-1,+∞)上的单调性,求N(0);
(2)求f(x)定义域上的最小值;
(3)是否存在实数m、n满足0≤m<n,使得f(x)在区间[m,n]上的值域也为[m,n]?
| 1 |
| 1+x |
| ln(1+x) |
| 1+x |
(1)令N(x)=(1+x)2-1+ln(1+x),判断并证明N(x)在(-1,+∞)上的单调性,求N(0);
(2)求f(x)定义域上的最小值;
(3)是否存在实数m、n满足0≤m<n,使得f(x)在区间[m,n]上的值域也为[m,n]?
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:计算题,存在型,分类讨论,函数的性质及应用,导数的综合应用
分析:(1)先对函数求导,由导函数在x>-1时的符号判断函数的单调性,代入求N(0)的值;
(2)直接求定义域,利用f(x)单调性求解函数f(x)的最小值;
(3)假设存在符合条件的m,n则有
,推导可判断m,n是否存在.
(2)直接求定义域,利用f(x)单调性求解函数f(x)的最小值;
(3)假设存在符合条件的m,n则有
|
解答:
解:(1)当x>-1时,N(x)=(1+x)2-1+ln(1+x),
N′(x)=2x+2+
>0,
所以N(x)在(-1,+∞)上是单调递增,且N(0)=0;
(2)f(x)的定义域是(-1,+∞),f′(x)=1-
,
当-1<x<0时,N(x)<0,所以,f′(x)<0,
当x>0时,N(x)>0,所以,f′(x)>0,
所以,在(-1,0)上f(x)单调递减,在(0,+∞)上,f(x)单调递增,
所以,fmin=f(0)=0;
(3)由(2)知f(x)在[0,+∞)上是单调递增函数,
若存在m,n满足条件,则必有f(m)=m,f(n)=n,
也即方程f(x)=x在[0,+∞)上有两个不等的实根m,n,
但方程f(x)=x,即
=0,只有一个实根x=0,
所以,不存在满足条件的实数m,n.
N′(x)=2x+2+
| 1 |
| 1+x |
所以N(x)在(-1,+∞)上是单调递增,且N(0)=0;
(2)f(x)的定义域是(-1,+∞),f′(x)=1-
| 1-ln(x+1) |
| (1+x)2 |
当-1<x<0时,N(x)<0,所以,f′(x)<0,
当x>0时,N(x)>0,所以,f′(x)>0,
所以,在(-1,0)上f(x)单调递减,在(0,+∞)上,f(x)单调递增,
所以,fmin=f(0)=0;
(3)由(2)知f(x)在[0,+∞)上是单调递增函数,
若存在m,n满足条件,则必有f(m)=m,f(n)=n,
也即方程f(x)=x在[0,+∞)上有两个不等的实根m,n,
但方程f(x)=x,即
| ln(x+1) |
| x+1 |
所以,不存在满足条件的实数m,n.
点评:本题考查了利用导数判断函数的单调性及求函数的最值问题,要注意分类讨论思想在解题中的运用.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
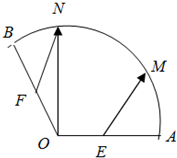 如图,扇形OAB的半径OA=2,∠AOB=120°,点E是OA的中点,点F是OB的中点,点M,N分别是
如图,扇形OAB的半径OA=2,∠AOB=120°,点E是OA的中点,点F是OB的中点,点M,N分别是