题目内容
对于直线m、n和平面α,下面命题中的真命题是( )
| A、如果m?α,n?α,m、n是异面直线,那么n∥α |
| B、如果m?α,n与α相交,那么m、n是异面直线 |
| C、如果m?α,n∥α,m、n共面,那么m∥n |
| D、如果m∥α,n∥α,m、n共面,那么m∥n |
考点:命题的真假判断与应用
专题:阅读型,空间位置关系与距离
分析:由线面的位置关系,即可判断A;由空间直线与直线的位置关系,即可判断B;
运用线面平行的性质定理,即可判断C;由线面平行的性质和直线与直线的位置关系,即可判断D.
运用线面平行的性质定理,即可判断C;由线面平行的性质和直线与直线的位置关系,即可判断D.
解答:
解:对于A.如果m?α,n?α,m、n是异面直线,则n∥α或n与α相交,故A错;
对于B.如果m?α,n与α相交,则m,n是相交或异面直线,故B错;
对于C.如果m?α,n∥α,m、n共面,由线面平行的性质定理,可得m∥n,故C对;
对于D.如果m∥α,n∥α,m,n共面,则m∥n或m,n相交,故D错.
故选C.
对于B.如果m?α,n与α相交,则m,n是相交或异面直线,故B错;
对于C.如果m?α,n∥α,m、n共面,由线面平行的性质定理,可得m∥n,故C对;
对于D.如果m∥α,n∥α,m,n共面,则m∥n或m,n相交,故D错.
故选C.
点评:本题考查空间直线与直线的位置关系和直线与平面的位置关系,考查线面平行的判定定理和性质定理及运用,考查空间想象能力,属于基础题和易错题.

练习册系列答案
相关题目
若函数f(x)在[14,20]上连续,且同时满足f(14)•f(20)<0,f(14)•f(17)>0,则( )
| A、f(x)在[14,17]上有零点 |
| B、f(x)在[17,20]上有零点 |
| C、f(x)在[14,17]上无零点 |
| D、f(x)在[17,20]上无零点 |
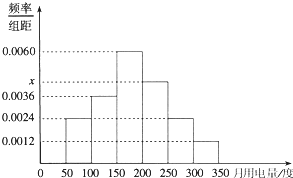 从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.求
从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.求