题目内容
已知正四棱台的上、下底面边长分别为1cm,3cm,侧棱长为2cm,则棱台的侧面积是 .
考点:棱柱、棱锥、棱台的侧面积和表面积
专题:空间位置关系与距离
分析:利用已知条件求出斜高,然后求解棱台的侧面积即可.
解答:
解:正四棱台的上、下底面边长分别为1cm,3cm,侧棱长为2cm,
所以棱台的斜高为:
=
.
所以棱台的侧面积是:4×
×
=8
.
故答案为:8
.
所以棱台的斜高为:
22-(
|
| 3 |
所以棱台的侧面积是:4×
| 1+3 |
| 2 |
| 3 |
| 3 |
故答案为:8
| 3 |
点评:本题列出棱台的侧面积的求法,考查空间想象能力以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
α,β是两个平面,l是直线,给出以下四个命题:
①若l⊥α,α⊥β,则l∥β,
②若l∥α,α∥β,则l∥β,
③l⊥α,α∥β,则l⊥β,
④l∥α,α⊥β,则l⊥β,
其中真命题有( )
①若l⊥α,α⊥β,则l∥β,
②若l∥α,α∥β,则l∥β,
③l⊥α,α∥β,则l⊥β,
④l∥α,α⊥β,则l⊥β,
其中真命题有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
对于直线m、n和平面α,下面命题中的真命题是( )
| A、如果m?α,n?α,m、n是异面直线,那么n∥α |
| B、如果m?α,n与α相交,那么m、n是异面直线 |
| C、如果m?α,n∥α,m、n共面,那么m∥n |
| D、如果m∥α,n∥α,m、n共面,那么m∥n |
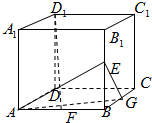 如图正方体ABCD-A1B1C1D1中,E、F、G分别是BB1、AB、BC的中点.
如图正方体ABCD-A1B1C1D1中,E、F、G分别是BB1、AB、BC的中点.