题目内容
不等式|x|≥a(x+1)对任意的实数x都成立,则实数a的取值范围是 .
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:由题意不等式|x|≥a(x+1)对任意的实数x都成立,讨论x+1、x与0的关系,两边除以x+1,分离出a,利用不等式的性质求最值,分别求出a的范围,最后求出交集即可.
解答:
解:由题意得,不等式|x|≥a(x+1),
①若-1<x<0,原不等式化为:a≤-
=-1+
,
又-1+
>0,则a≤0,
②若x≥0时,原不等式化为:a≤
=1-
又1-
≥0,则a≤0,
③若x<-1,原不等式化为:a≥-
=-1+
,
又-1+
<-1,则a≥-1,
④若x=-1,则有1≥0,恒成立;
∵不等式|x|≥a(x+1)对任意的实数x都成立,
∴以上情况取交集得,a∈[-1,0],
故答案为:[-1,0].
①若-1<x<0,原不等式化为:a≤-
| x |
| x+1 |
| 1 |
| x+1 |
又-1+
| 1 |
| x+1 |
②若x≥0时,原不等式化为:a≤
| x |
| x+1 |
| 1 |
| x+1 |
又1-
| 1 |
| x+1 |
③若x<-1,原不等式化为:a≥-
| x |
| x+1 |
| 1 |
| x+1 |
又-1+
| 1 |
| x+1 |
④若x=-1,则有1≥0,恒成立;
∵不等式|x|≥a(x+1)对任意的实数x都成立,
∴以上情况取交集得,a∈[-1,0],
故答案为:[-1,0].
点评:本题考查绝对值不等式的解法,恒成立问题,运用了分类讨论的思想,解题的关键是去掉绝对值,利用常数分离法进行求解,利用不等式的性质求最值,此类题目是高考常见的题型.

练习册系列答案
相关题目
对于直线m、n和平面α,下面命题中的真命题是( )
| A、如果m?α,n?α,m、n是异面直线,那么n∥α |
| B、如果m?α,n与α相交,那么m、n是异面直线 |
| C、如果m?α,n∥α,m、n共面,那么m∥n |
| D、如果m∥α,n∥α,m、n共面,那么m∥n |
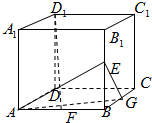 如图正方体ABCD-A1B1C1D1中,E、F、G分别是BB1、AB、BC的中点.
如图正方体ABCD-A1B1C1D1中,E、F、G分别是BB1、AB、BC的中点. 一个三棱柱的底面是正三角形,侧面垂直于底面,它的三视图及其尺寸如图(单位:cm).则该三棱柱的表面积为
一个三棱柱的底面是正三角形,侧面垂直于底面,它的三视图及其尺寸如图(单位:cm).则该三棱柱的表面积为