Question

某中学为了解高三女生的身高状况，随机抽取了100名女生．按身高分组得到频率分布表为：

组号	分组	频数	频率
A组	[150，155）	5	0.050
B组	[155，160）	m	0.350
C组	[160，165）	30	n
D组	[165，170）	x	0.200
E组	[170，175）	10	0.100

（Ⅰ）求表中的m，n，x的值，并画出频率分布直方图；
（Ⅱ）由于该校要组成女子篮球队，决定在C、D、E组中用分层抽样方法抽取6人，求各组抽取的人数；
（Ⅲ）在（Ⅱ）中被抽取的6人中，随机抽取2名队员，求C组中选中人数ξ的分布列和数学期望．

Answer 1

考点：离散型随机变量的期望与方差,频率分布直方图,离散型随机变量及其分布列

专题：概率与统计

分析：（Ⅰ）根据频率=

频数

样本容量

，计算即可，并绘制直方图，
（Ⅱ）根据分层抽样的原则，由已知条件能分别求出各组抽取的人数；
（Ⅲ）由已知得C组中选中人数ξ的可能取值为0，1，2，分别求出相应的概率，由此能求出ξ的分布列和数学期望．

解答： 解：（Ⅰ）m=100×0.35=35，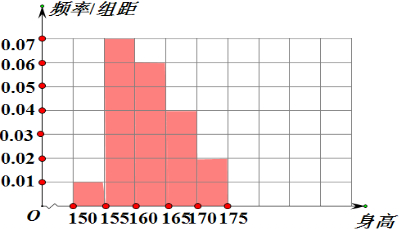
n=

30

100

=0.3，x=100×0.2=20，
频率分布直方图如右图所示：
（Ⅱ）∵C、D、E组三组共60人，利用分层抽样的方法抽取6人，
则C组应抽取人数为：

30

60

×6=3人，
D组应抽取人数为：

20

60

×6=2人，
E组应抽取人数为：

10

60

×6=1人．
（Ⅲ）由已知得C组中选中人数ξ的可能取值为0，1，2，
P（ξ=0）=

C 0 3 C 2 3

C 2 6

=

1

5

，
P（ξ=1）=

C 1 3 C 1 3

C 2 6

=

3

5

，
P（ξ=2）=

C 2 3 C 0 3

C 2 6

=

1

5

，
∴ξ的分布列为：

ξ	0	1	2
P	1 5	3 5	1 5

Eξ=0×

1

5

+1×

3

5

+2×

1

5

=1．

点评：本题考查概率的求法，考查离散型随机变量的分布列和数学期望的求法，考查了频率分布直方图，以及古典概型概率的问题，是中档题，解题时要认真审题，在历年高考中都是必考题型之一．