题目内容
7.已知f(x)是偶函数,它在[0,+∞)上是减函数,若f(ex)≥f(-e),则x的取值范围是( )| A. | R | B. | (-∞,-1]∪[1,+∞) | C. | (-∞,1] | D. | [-1,1] |
分析 根据题意,由函数奇偶性的性质可以将不等式f(ex)≥f(-e)等价为f(|ex|)≥f(|-e|),进而可以转化为|ex|≤|-e|,即ex≤e,解可得答案.
解答 解:根据题意,f(x)是偶函数,且在[0,+∞)上是减函数,
则不等式f(ex)≥f(-e),等价为f(|ex|)≥f(|-e|),
又由f(x)在[0,+∞)上是减函数,
则有|ex|≤|-e|,即ex≤e,
解可得x≤1,
即x的取值范围是(-∞,1];
故选:C.
点评 本题考查奇偶性与单调性的综合运用,解决这一类问题是要注意培养数形结合的思想方法.

练习册系列答案
相关题目
2.若f(t)=$\frac{t}{cosx}$,则f′(t)等于( )
| A. | $\frac{t}{co{s}^{2}x}$ | B. | -$\frac{t}{co{s}^{2}x}$ | C. | $\frac{1}{cosx}$ | D. | $\frac{t}{sinx}$ |
19.已知cos2α=$\frac{1}{3}$,则$\frac{tan2α}{tanα}$的值为( )
| A. | -4 | B. | -$\frac{1}{4}$ | C. | 4 | D. | $\frac{1}{4}$ |
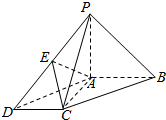 在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,点E是PD的中点.
在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,点E是PD的中点.