题目内容
已知正四棱锥S-ABCD的所有棱长都等于a,过不相邻的两条侧棱作截面SAC,则截面面积为 .
考点:棱锥的结构特征
专题:空间位置关系与距离
分析:按照正四棱锥的定义,求出棱锥的高,然后求解截面PAC的面积.
解答:
解:正四棱锥S-ABCD的所有棱长都是a,
∴AC=
a,SO=
=
a,
则截面SAC的面积为:
×
a×
a=
a2.
故答案为:
a2.
∴AC=
| 2 |
a2-(
|
| ||
| 2 |
则截面SAC的面积为:
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查正棱锥的定义的理解与应用,几何体的面积的求法,考查空间想象能力以及计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
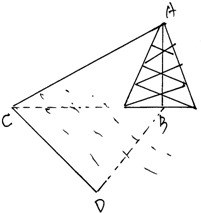 如图所示,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A的仰角为θ,则塔高AB=
如图所示,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A的仰角为θ,则塔高AB=