题目内容
如图甲、乙所示，回答下列问题．
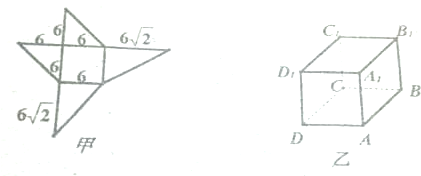
（1）沿图中虚线将它们折叠起来，是哪一种几何体，试用文字描述．
（2）需要多少个这样的几何体才能拼成一个棱长为6cm的长方体？
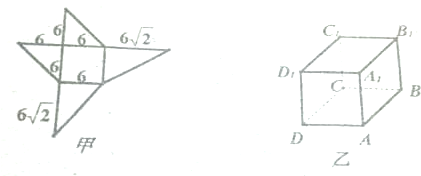
（1）沿图中虚线将它们折叠起来，是哪一种几何体，试用文字描述．
（2）需要多少个这样的几何体才能拼成一个棱长为6cm的长方体？
考点：表面展开图
专题：空间位置关系与距离
分析：根据题意将图形折叠起来，画其直观图为一个有一条侧棱垂直于底面的四棱锥，然后利用棱锥的体积公式可求得其体积；画出棱长为6的正方体，找出四棱锥的个数即可．
解答：
解：（1）它是有一条侧棱垂直于底面的四棱锥（如图）．（注：评分注意实线、虚线；垂直关系；长度比例等）
（2）PD⊥AD，PD⊥CD，
∴PD⊥平面ABCD，则VP-ABCD=
×6×6×6=72
需要3个这样的几何体可以拼成一个正方体．
就是C1-ABCD，C1-A1B1BA，C1-ADD1A1；三个四棱锥．
（2）PD⊥AD，PD⊥CD，∴PD⊥平面ABCD，则VP-ABCD=
| 1 |
| 3 |
需要3个这样的几何体可以拼成一个正方体．
就是C1-ABCD，C1-A1B1BA，C1-ADD1A1；三个四棱锥．
点评：本题是基础题，考查几何体的体积的计算，考查空间想象能力．
练习册系列答案
相关题目
设全集U=R，集合A={x|x≥0}，B={x|-1＜x＜3}，则（∁UA）∩B=（ ）
| A、{x|-1＜x＜0} |
| B、{x|0＜x＜1} |
| C、{x|-3＜x＜0} |
| D、{x|x≥3} |
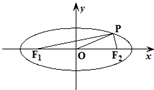如图，F1、F2是椭圆