题目内容

蒸汽机飞轮的直径为1.4m，以每小时按逆时针方向旋转2400转．求：
（1）飞轮每秒钟转过的弧度数；
（2）轮周上一点每秒钟经过的弧长．
考点：弧长公式
专题：计算题
分析：首先求出每1s转过的弧度数，然后利用弧长公式即可得出答案．
解答： 解：因为飞轮转速2400转/小时=
2
3
转/秒，而且飞轮作逆时针旋转，
（1）所以它每1s转过的弧度数为
2
3
×2π=
4π
3
．
（2）轮上一点每1s所转过的弧长为 L=αr=
4π
3
×0.7=
14π
15
米．
点评：本题考查了弧长公式，解题的关键是将实际问题转化成数学问题，此题比较简单，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=
6x    (x≥0)
2x    (x＜0)
则f（f（-1））=
 
．
已知B（-3，0），C（3，0），△ABC中BC边上的高为3，求△ABC的垂心H的轨迹方程．
已知正四棱锥S-ABCD的所有棱长都等于a，过不相邻的两条侧棱作截面SAC，则截面面积为
 
．
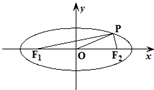如图，F1、F2是椭圆
x2
a2
+
y2
b2
=1的两个焦点，O为坐标原点，P是椭圆上的一点，且满足|F1F2|=2|OP|，若∠PF2F1=5∠PF1F2，则椭圆的离心率为（　　）
A、
3
2
B、
6
3
C、
2
2
D、
2
3
截至到1999年底，我国人口约为13亿．如果今后能将人口年平均增长率控制在1%．
（1）那么在过20年后，我过人口数最多为多少？（精确到亿）
（2）再过多少年我过人口总数达到18亿？（取整数）
参考数据如下：
1.0119=1.208，1.0120=1.22，1.0121=1.232
log1018=1.2553，log1013=1.1139，log101.01=0.0043．
计算：
(1-lg5)2+lg2•lg5
lg8
=
 
．
下列叙述中：
①函数f（x）=xα（α∈R）的图象可能通过坐标系中任何一个象限；
②函数f（x）=loga（mx2-mx+1）（a＞0，a≠1）定义域为R，则m∈（0，4）；
③若min{m，n}=
m (m≤n)
n (m＞n)
，则函数f（x）=min{x
1
3
，2x-2，1-3x}存在最大值；
④函数f（x）=loga（ax-1）（a＞0，a≠1）在定义域内单调递增；
⑤已知函数f（x）=x3+bx+cloga（
x2+1
+x）+2（a＞0，a≠1，b，c∈R），若x＞0时，f（x）≥5，则x＜0时，有f（x）≤-1．
其中，正确命题的序号是
 
．
已知方程x2+（2+a）x+1+a+b=0的两根是x1，x2，且0＜x1＜1＜x2，则
b
a
的取值范围是（　　）
A、（-2，-
2
3
）
B、[-2，-
2
3
）
C、（-1，-
2
3
）
D、（-2，-1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网