题目内容
已知a1=2,an=2-
.
(1)求证bn=
为等差数列;
(2)求cn=
的前n项和Tn.
| 1 |
| an-1 |
(1)求证bn=
| 1 |
| an-1 |
(2)求cn=
| 1 |
| bn•bn+1 |
考点:数列的求和,等差关系的确定
专题:等差数列与等比数列
分析:(1)由已知条件推导出an-1=1-
=
,从而得到
-
=1,由此能证明数列{bn}是以1为首项,1为公差的等差数列.
(2)cn=
=
=
-
,由此利用裂项求和法能求出cn=
的前n项和Tn.
| 1 |
| an-1 |
| an-1-1 |
| an-1 |
| 1 |
| an-1 |
| 1 |
| an-1-1 |
(2)cn=
| 1 |
| bn•bn+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n-1 |
| 1 |
| bn•bn-1 |
解答:
(1)证明:∵a1=2,an=2-
,
∴an-1=1-
=
,
∴
=
=
=1+
,
∴
-
=1,
∵
=1,bn=
,
∴数列{bn}是以1为首项,1为公差的等差数列.
(2)解:∵数列{bn}是以1为首项,1为公差的等差数列,
∴bn=1+(n-1)×1=n,
∴cn=
=
=
-
,
∴Tn=1-
+
-
+…+
-
=1-
=
.
| 1 |
| an-1 |
∴an-1=1-
| 1 |
| an-1 |
| an-1-1 |
| an-1 |
∴
| 1 |
| an-1 |
| an-1 |
| an-1-1 |
| an-1-1+1 |
| an-1-1 |
| 1 |
| an-1-1 |
∴
| 1 |
| an-1 |
| 1 |
| an-1-1 |
∵
| 1 |
| a1-1 |
| 1 |
| an-1 |
∴数列{bn}是以1为首项,1为公差的等差数列.
(2)解:∵数列{bn}是以1为首项,1为公差的等差数列,
∴bn=1+(n-1)×1=n,
∴cn=
| 1 |
| bn•bn+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n-1 |
∴Tn=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
=
| n |
| n+1 |
点评:本题考查等差数列的证明,考查数列的前n项和的求法,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
相关题目
2sin105°cos105°的值为( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
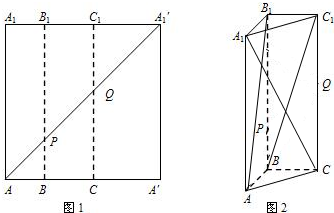 已知矩形纸片AA′A1′A1,点B、C、B1、C1分别为AA′、A1A1′的三等分点,将矩形纸片沿BB1、CC1折成图2所示的三棱柱ABC-A1B1C1,若面对角线AB1⊥BC1,求证:A1C⊥AB1.
已知矩形纸片AA′A1′A1,点B、C、B1、C1分别为AA′、A1A1′的三等分点,将矩形纸片沿BB1、CC1折成图2所示的三棱柱ABC-A1B1C1,若面对角线AB1⊥BC1,求证:A1C⊥AB1.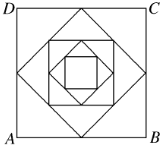 如图,正方形ABCD的边长是a,依次连接正方形ABCD各边中点得到一个新的正方形,再依次连接新正方形各边中点又得到一个新的正方形,依此得到一系列的正方形,如图所示.现有一只小虫从A点出发,沿正方形的边逆时针方向爬行,每遇到新正方形的顶点时,沿这个正方形的边逆时针方向爬行,如此下去,问爬行2n条线段的长度的平方和是多少?
如图,正方形ABCD的边长是a,依次连接正方形ABCD各边中点得到一个新的正方形,再依次连接新正方形各边中点又得到一个新的正方形,依此得到一系列的正方形,如图所示.现有一只小虫从A点出发,沿正方形的边逆时针方向爬行,每遇到新正方形的顶点时,沿这个正方形的边逆时针方向爬行,如此下去,问爬行2n条线段的长度的平方和是多少?