题目内容
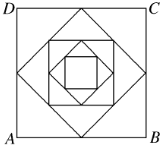 如图,正方形ABCD的边长是a,依次连接正方形ABCD各边中点得到一个新的正方形,再依次连接新正方形各边中点又得到一个新的正方形,依此得到一系列的正方形,如图所示.现有一只小虫从A点出发,沿正方形的边逆时针方向爬行,每遇到新正方形的顶点时,沿这个正方形的边逆时针方向爬行,如此下去,问爬行2n条线段的长度的平方和是多少?
如图,正方形ABCD的边长是a,依次连接正方形ABCD各边中点得到一个新的正方形,再依次连接新正方形各边中点又得到一个新的正方形,依此得到一系列的正方形,如图所示.现有一只小虫从A点出发,沿正方形的边逆时针方向爬行,每遇到新正方形的顶点时,沿这个正方形的边逆时针方向爬行,如此下去,问爬行2n条线段的长度的平方和是多少?考点:数列的求和
专题:应用题,等差数列与等比数列
分析:根据中位线定理,每一次连接得到的正方形的边长是上一个正方形对角线的一半,即可得到第一、二、三次连接得到的正方形的边长,依此类推找出规律,可得出第n次围出的正方形的边长,再由题意和运用等比数列的前n项和公式即可.
解答:
解:由题意得,每一次连接得到的正方形的边长是上一个正方形对角线的一半,
根据中位线定理得:
第一次连接得到的正方形的边长为
a,第二次连接得出的正方形的边长为(
)2a=
a,
第三次次连接得出的正方形的边长为
a,…
综上可得第2n次围出的正方形边长为(
)2na.
由题意知,一只小虫在每个正方形爬行的线段的长度是此正方形的边长的一半,
所求的2n条线段的长度的平方和是:
s=
{(
a)2+[(
)2a]2+(
a)2+…+[(
)2na]2}
=
[1+(
)2+(
)4+…+(
)2(2n-1)]=
×
=
•[1-(
)n].
根据中位线定理得:
第一次连接得到的正方形的边长为
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
第三次次连接得出的正方形的边长为
| ||
| 4 |
综上可得第2n次围出的正方形边长为(
| ||
| 2 |
由题意知,一只小虫在每个正方形爬行的线段的长度是此正方形的边长的一半,
所求的2n条线段的长度的平方和是:
s=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 4 |
| ||
| 2 |
=
| a2 |
| 4 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| a2 |
| 4 |
1-(
| ||
1-
|
| a2 |
| 2 |
| 1 |
| 4 |
点评:本题以图形的变化为载体,考查了归纳推理的应用,中位线定理,等比数列的前n项和公式,解题的关键是通过观察、归纳与总结,得到其中的规律,求出第n次围出的正方形的边长.

练习册系列答案
相关题目
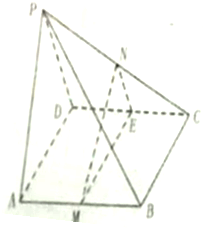 在四棱锥P-ABCD中,ABCD是矩形,PA⊥平面ABCD,M、N、E分别是AB、PC、CD的中点.
在四棱锥P-ABCD中,ABCD是矩形,PA⊥平面ABCD,M、N、E分别是AB、PC、CD的中点.