题目内容
选修4-4:极坐标与参数方程选讲:在平面直角坐标系xOy中,直线l的参数方程为
(t为参数),以该直角坐标系的原点O为极点,x轴的正半轴为极轴的极坐标系下,圆C的极坐标方程为ρ=-2cosθ+2
sinθ
(1)求直线l的普通方程和圆C的直角坐标方程;
(2)设点P的直角坐标为(-2,
),直线l与圆C相交于两点A,B两点,求|PA|•|PB|的值.
|
| 3 |
(1)求直线l的普通方程和圆C的直角坐标方程;
(2)设点P的直角坐标为(-2,
| 3 |
考点:参数方程化成普通方程,直线与圆锥曲线的综合问题
专题:坐标系和参数方程
分析:(1)根据直线的参数方程,消去参数得到普通方程,借助于极坐标方程和直角坐标方程的互化公式进行化简即可;
(2)首先,联立方程组,得到4x2+2x-3=0,设A(x1,y1),B(x2,y2),得到x1+x2=-
,x1x2=-
,然后,结合两点间的距离公式进行求解即可.
(2)首先,联立方程组,得到4x2+2x-3=0,设A(x1,y1),B(x2,y2),得到x1+x2=-
| 1 |
| 2 |
| 3 |
| 4 |
解答:
解:(1)根据直线l的参数方程为
(t为参数),
得
x-y+
=0,
根据圆C的极坐标方程为ρ=-2cosθ+2
sinθ,得
x2+y2=-2x+2
y,
∴(x+1)2+(y-
)2=4,
(2)联立方程组
,得
4x2+2x-3=0,设A(x1,y1),B(x2,y2)
∴x1+x2=-
,x1x2=-
,
∴|PA|•|PB|=
•
=
•
=
•
=
=
=
.
∴|PA|•|PB|=
.
|
得
| 3 |
| 3 |
根据圆C的极坐标方程为ρ=-2cosθ+2
| 3 |
x2+y2=-2x+2
| 3 |
∴(x+1)2+(y-
| 3 |
(2)联立方程组
|
4x2+2x-3=0,设A(x1,y1),B(x2,y2)
∴x1+x2=-
| 1 |
| 2 |
| 3 |
| 4 |
∴|PA|•|PB|=
(x1+2)2+(y1-
|
(x2+2)2+(y2-
|
=
| 4x12+2x1-3+2x1+7 |
| 4x22+2x2-3+2x2+7 |
=
| 2x1+7 |
| 2x2+7 |
=
| 4x1x2+14(x1+x2)+49 |
=
4×(-
|
=
| 39 |
∴|PA|•|PB|=
| 39 |
点评:本题重点考查了直线的参数方程和普通方程的互化、极坐标方程和直角坐标方程的互化、直线与圆的位置关系等知识,属于中档题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
方程
+
=2表示( )
| (x+1)2+y2 |
| (x-1)2+y2 |
| A、椭圆 | B、圆 | C、直线 | D、线段 |
如图,在△ABC中,AB=3,AC=4,BC=5,AD平分∠BAC,则BD的值为( )
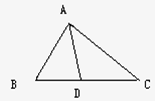

A、
| ||
B、
| ||
C、
| ||
D、
|
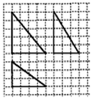 如图,格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体最长的棱的长度等于( )
如图,格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体最长的棱的长度等于( )A、
| ||
B、
| ||
C、5
| ||
D、2
|