题目内容
长方体ABCD-A1B1C1D1的各个顶点都在表面积为16π的球O的球面上,其中AB:AD:AA1=2:1:
,则四棱锥O-ABCD的体积为( )
| 3 |
A、
| ||||
B、
| ||||
C、2
| ||||
| D、3 |
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:由已知得球O的半径R=2,设AB=2k,AD=k,AA1=
k,则(2k)2+k2+(
k)2=(2R)2=16,得到AB=2
,AD=
,AA1=
,由此能求出四棱锥O-ABCD的体积.
| 3 |
| 3 |
| 2 |
| 2 |
| 6 |
解答:
解:设球O的半径为R,16π=4πR2,R=2,2R=4,
设AB=2k,AD=k,AA1=
k,
(2k)2+k2+(
k)2=(2R)2=16,
解得k=
,
∴AB=2
,AD=
,AA1=
,
四棱锥O-ABCD的底面积S=AB×AD=4,
高h=
AA1=
,
四棱锥O-ABCD的体积V=
×4×
=
.
故选:A.
设AB=2k,AD=k,AA1=
| 3 |
(2k)2+k2+(
| 3 |
解得k=
| 2 |
∴AB=2
| 2 |
| 2 |
| 6 |
四棱锥O-ABCD的底面积S=AB×AD=4,
高h=
| 1 |
| 2 |
| ||
| 2 |
四棱锥O-ABCD的体积V=
| 1 |
| 3 |
| ||
| 2 |
2
| ||
| 3 |
故选:A.
点评:本题考查四棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
设a、b∈z,且a≠0,则(a-b)a2<0,且a<b的( )条件.
| A、充分不必要 |
| B、必要而不充分 |
| C、充要 |
| D、既不充分也不必要 |
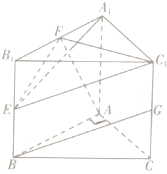 已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AA1=AC=AB,∠BAC=90°,点E,F,G分别是棱BB1,A1B1,CC1的中点.求证:AF⊥BG.
已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AA1=AC=AB,∠BAC=90°,点E,F,G分别是棱BB1,A1B1,CC1的中点.求证:AF⊥BG.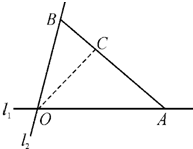 如图,在C城周边已有两条公路l1,l2在点O处交汇,且它们的夹角为75°.已知OC=(
如图,在C城周边已有两条公路l1,l2在点O处交汇,且它们的夹角为75°.已知OC=(