题目内容
判断下列说法正确的是 .
①在直线y=xtanα+3中,斜率k=tanα,α为倾斜角
②过点(x1,y1),(x2,y2)所有直线方程为(x2-x1)(y-y1)=(y2-y1)(x-x1)
③a,b为异面直线,与a,b都相交的两条直线l1,l2不可能相交.
④y=
+
的最小值为5.
⑤P是△ABC所在平面外一点,若点P到三角形的三个顶点的距离相等,则P点的射影为△ABC的外心.
①在直线y=xtanα+3中,斜率k=tanα,α为倾斜角
②过点(x1,y1),(x2,y2)所有直线方程为(x2-x1)(y-y1)=(y2-y1)(x-x1)
③a,b为异面直线,与a,b都相交的两条直线l1,l2不可能相交.
④y=
| x2-8x+20 |
| x2+1 |
⑤P是△ABC所在平面外一点,若点P到三角形的三个顶点的距离相等,则P点的射影为△ABC的外心.
考点:命题的真假判断与应用
专题:直线与圆,简易逻辑
分析:①,在直线y=xtanα+3中,斜率k=tanα,α不一定为倾斜角,可判断①;
②,分l⊥x轴与l不与x轴垂直两类讨论,可得过点(x1,y1),(x2,y2)所有直线方程为(x2-x1)(y-y1)=(y2-y1)(x-x1),可判断②;
③,利用反证法可证得与异面直线a,b都相交的两条直线l1,l2不可能相交,可判断③
④,利用y=
+
的几何意义,可判断④.
⑤,P是△ABC所在平面外一点,若点P到三角形的三个顶点的距离相等⇒P点的射影O到△ABC的各顶点的距离相等,可判断⑤.
②,分l⊥x轴与l不与x轴垂直两类讨论,可得过点(x1,y1),(x2,y2)所有直线方程为(x2-x1)(y-y1)=(y2-y1)(x-x1),可判断②;
③,利用反证法可证得与异面直线a,b都相交的两条直线l1,l2不可能相交,可判断③
④,利用y=
| x2-8x+20 |
| x2+1 |
⑤,P是△ABC所在平面外一点,若点P到三角形的三个顶点的距离相等⇒P点的射影O到△ABC的各顶点的距离相等,可判断⑤.
解答:
解:对于①,在直线y=xtanα+3中,斜率k=tanα,α为倾斜角,①正确;
对于②,过点(x1,y1),(x2,y2)的直线l的方程:
当l⊥x轴时,x=x1=x2,满足(x2-x1)(y-y1)=(y2-y1)(x-x1);
当l不与x轴垂直时,l的方程为:y-y1=
(x-x1),满足(x2-x1)(y-y1)=(y2-y1)(x-x1);
所以,所有直线方程为(x2-x1)(y-y1)=(y2-y1)(x-x1),即②正确;
对于③,a,b为异面直线,与a,b都相交的两条直线l1,l2不可能相交,③正确,
理由如下:假设l1,l2相交,则l1,l2共面,于是可得直线a与直线b共面,与a,b为异面直线矛盾,故直线l1,l2不可能相交;
对于④,y=
+
的几何意义为:数轴上的点A(x,0)到点M(4,2)与N点(0,1)的距离之和,
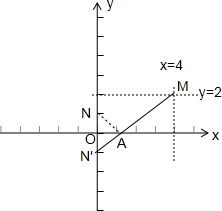
设点N关于x轴的对称点为N′,则|MA|+|AN|=|MA|+|AN′|≥|MN′|(当且仅当M、A、N′三点共线时取“=”),
即y=
+
≥|MN′|=
=5,其最小值为5,④正确.
对于⑤,P是△ABC所在平面外一点,若点P到三角形的三个顶点的距离相等,则P点的射影O到△ABC的各顶点的距离相等,所以O为△ABC的外心,⑤正确.
故答案为:①②④⑤.
对于②,过点(x1,y1),(x2,y2)的直线l的方程:
当l⊥x轴时,x=x1=x2,满足(x2-x1)(y-y1)=(y2-y1)(x-x1);
当l不与x轴垂直时,l的方程为:y-y1=
| y2-y1 |
| x2-x1 |
所以,所有直线方程为(x2-x1)(y-y1)=(y2-y1)(x-x1),即②正确;
对于③,a,b为异面直线,与a,b都相交的两条直线l1,l2不可能相交,③正确,
理由如下:假设l1,l2相交,则l1,l2共面,于是可得直线a与直线b共面,与a,b为异面直线矛盾,故直线l1,l2不可能相交;
对于④,y=
| x2-8x+20 |
| x2+1 |
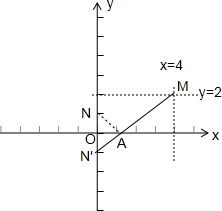
设点N关于x轴的对称点为N′,则|MA|+|AN|=|MA|+|AN′|≥|MN′|(当且仅当M、A、N′三点共线时取“=”),
即y=
| x2-8x+20 |
| x2+1 |
| 42+(2-(-1))2 |
对于⑤,P是△ABC所在平面外一点,若点P到三角形的三个顶点的距离相等,则P点的射影O到△ABC的各顶点的距离相等,所以O为△ABC的外心,⑤正确.
故答案为:①②④⑤.
点评:本题考查命题的真假判断与应用,综合考查直线的方程、空间直线的位置关系、函数表达式的几何意义的应用,属于中档题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
已知抛物线x2=2py(p>0)的焦点为F,A,B,C都是抛物线上的点,满足
+
+
=
,则kAB+kBC+kAC=( )
| FA |
| FB |
| FC |
| 0 |
| A、0 | ||
B、
| ||
| C、1 | ||
| D、不能确定 |
如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计众数与中位数分别是( ) 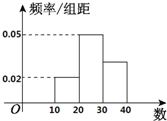

| A、25;25 |
| B、26;25 |
| C、26;26 |
| D、25;26 |
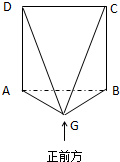 如图,四棱锥G-ABCD中,ABCD是正方形,且边长为2a,面ABCD⊥面ABG,AG=BG.
如图,四棱锥G-ABCD中,ABCD是正方形,且边长为2a,面ABCD⊥面ABG,AG=BG.